SPSS操作总结

数据准备
数据随机分组
现将数据导入到SPSS。
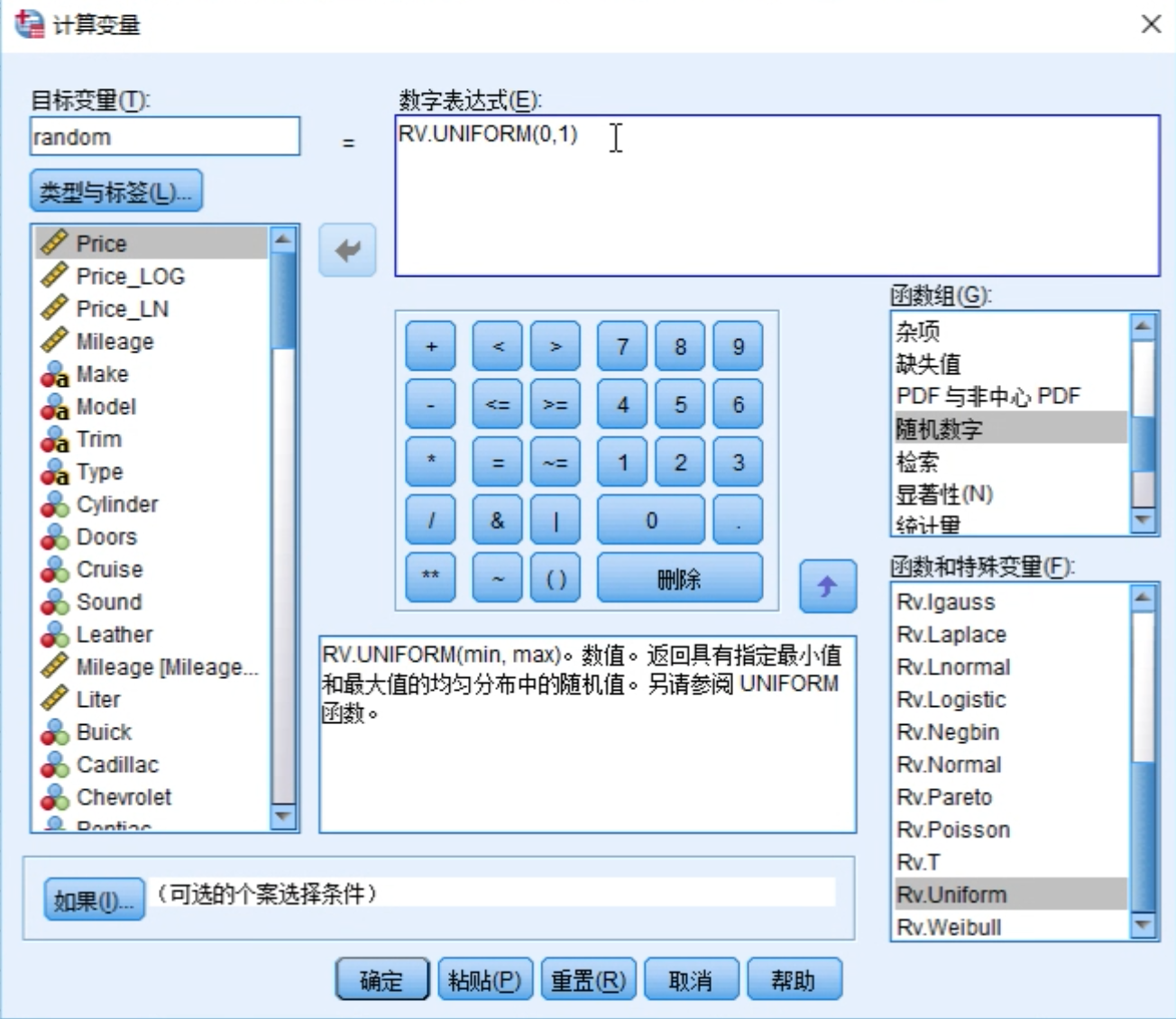
选择计算变量,生成随机数,用来作为数据分组的依据。

新的随机数字段

对数据进行分组排序

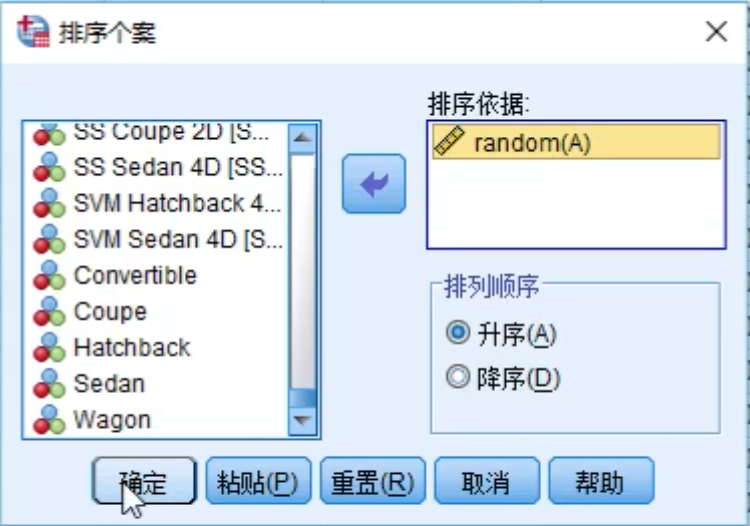
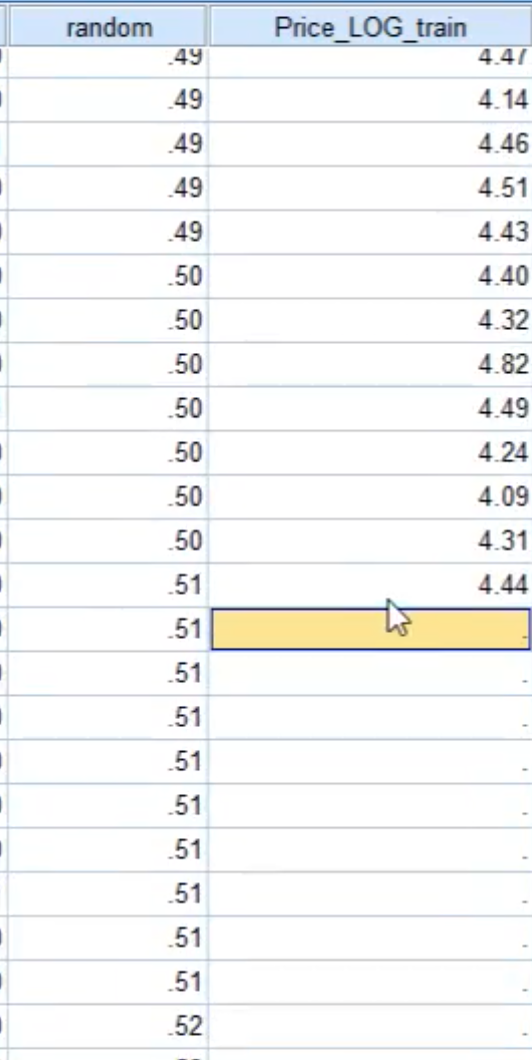
训练集与检验集分离
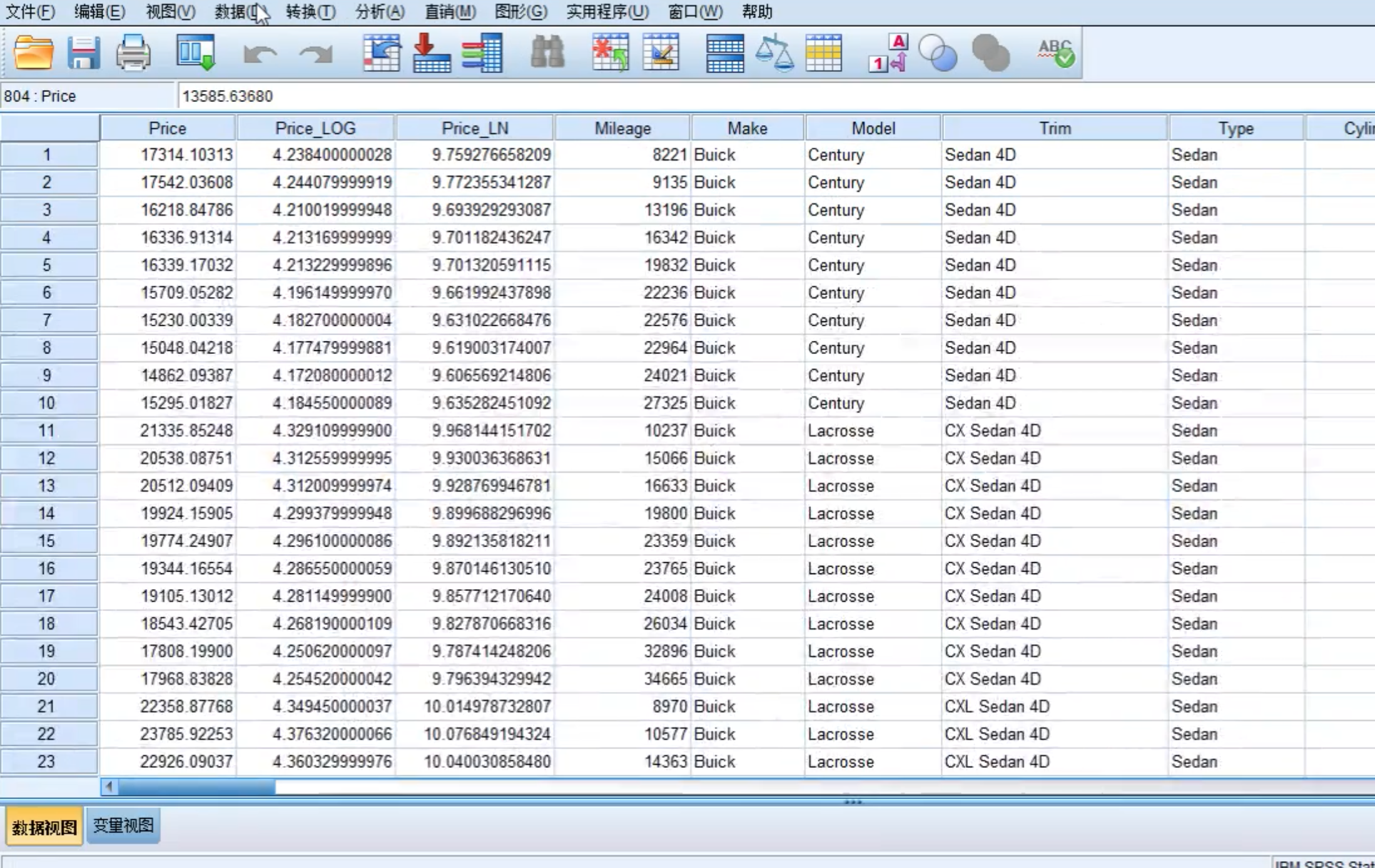
总数据804条,这里对数据进行随机打散排序后,将其中的前一半(402条)作为训练集,后一半(402条)作为检验集。

新增一列计算变量Price_LOG_train(即复制已有的列Price_Log),删除该列中从第403条到最后的数值,这样就产生了检验集数据。
线性回归
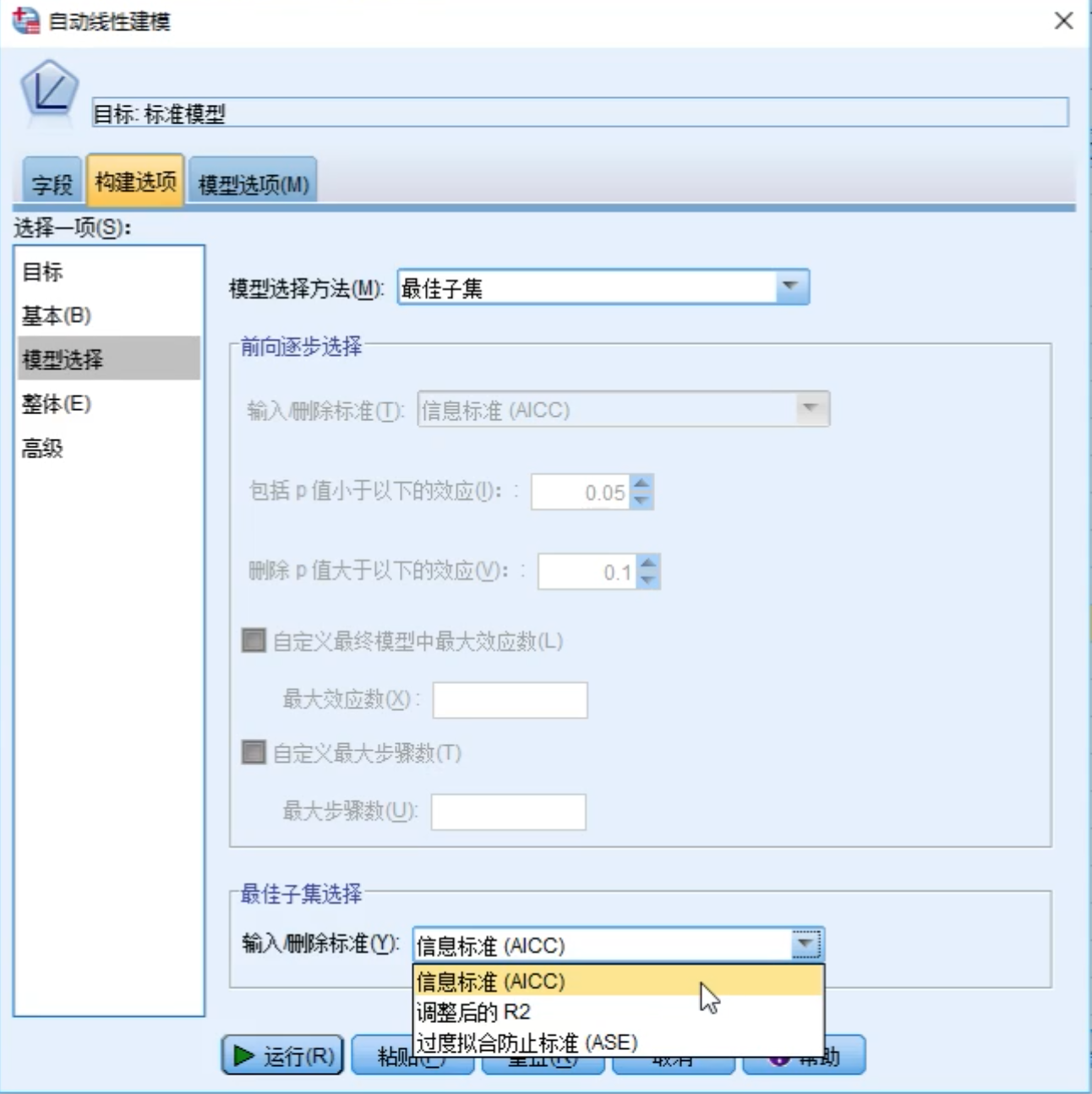
最优子集回归
做最优子集回归的目的是要确定哪些自变量是对因变量”有用”的,以便在后面做进一步回归时选择这些“最优”的变量。

选型因变量和要评估的自变量
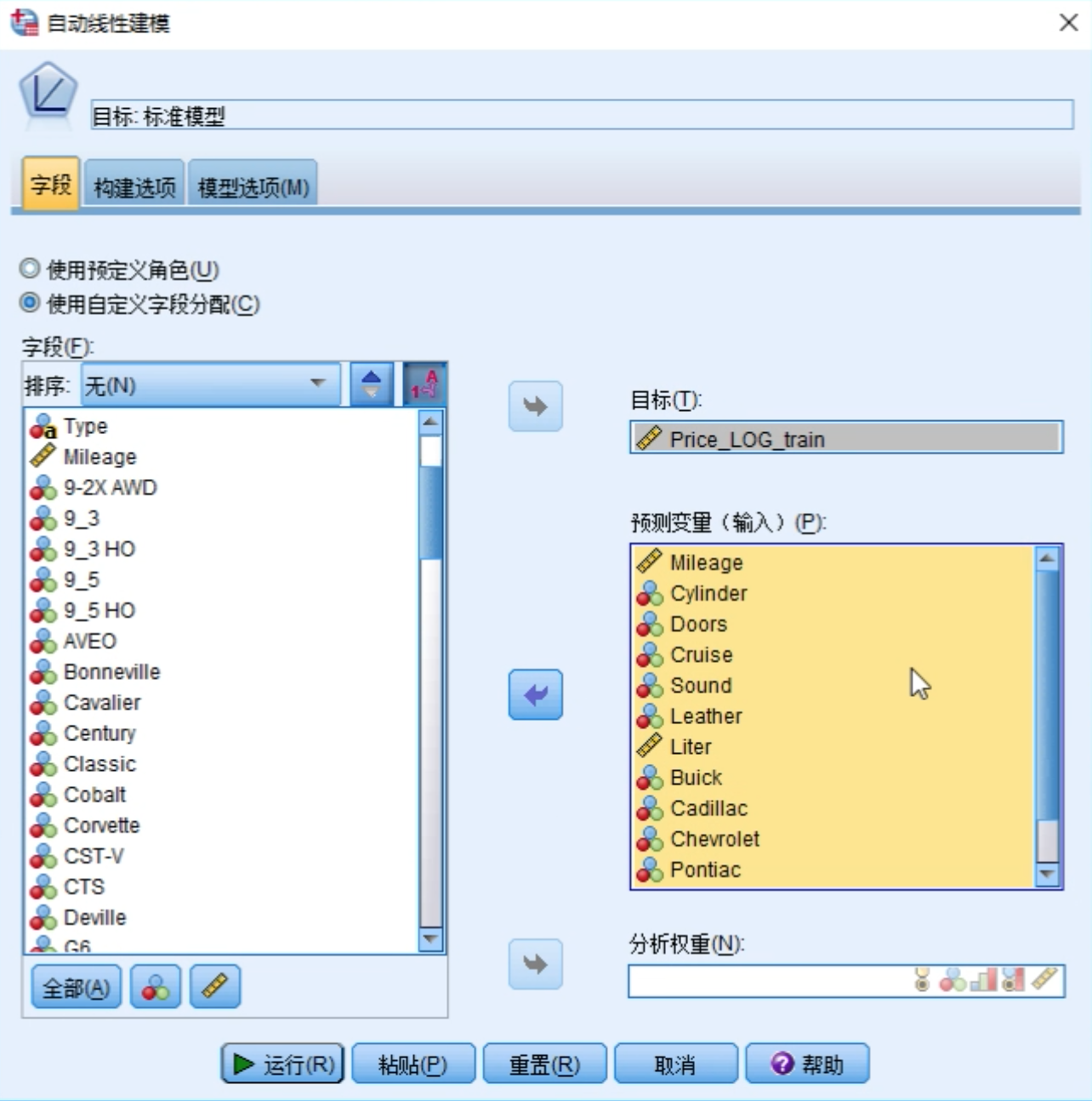
使用最优子集作为建模方法,点击运行按钮。
从结果中可以看到刚才挑选的自变量对因变量的重要性。
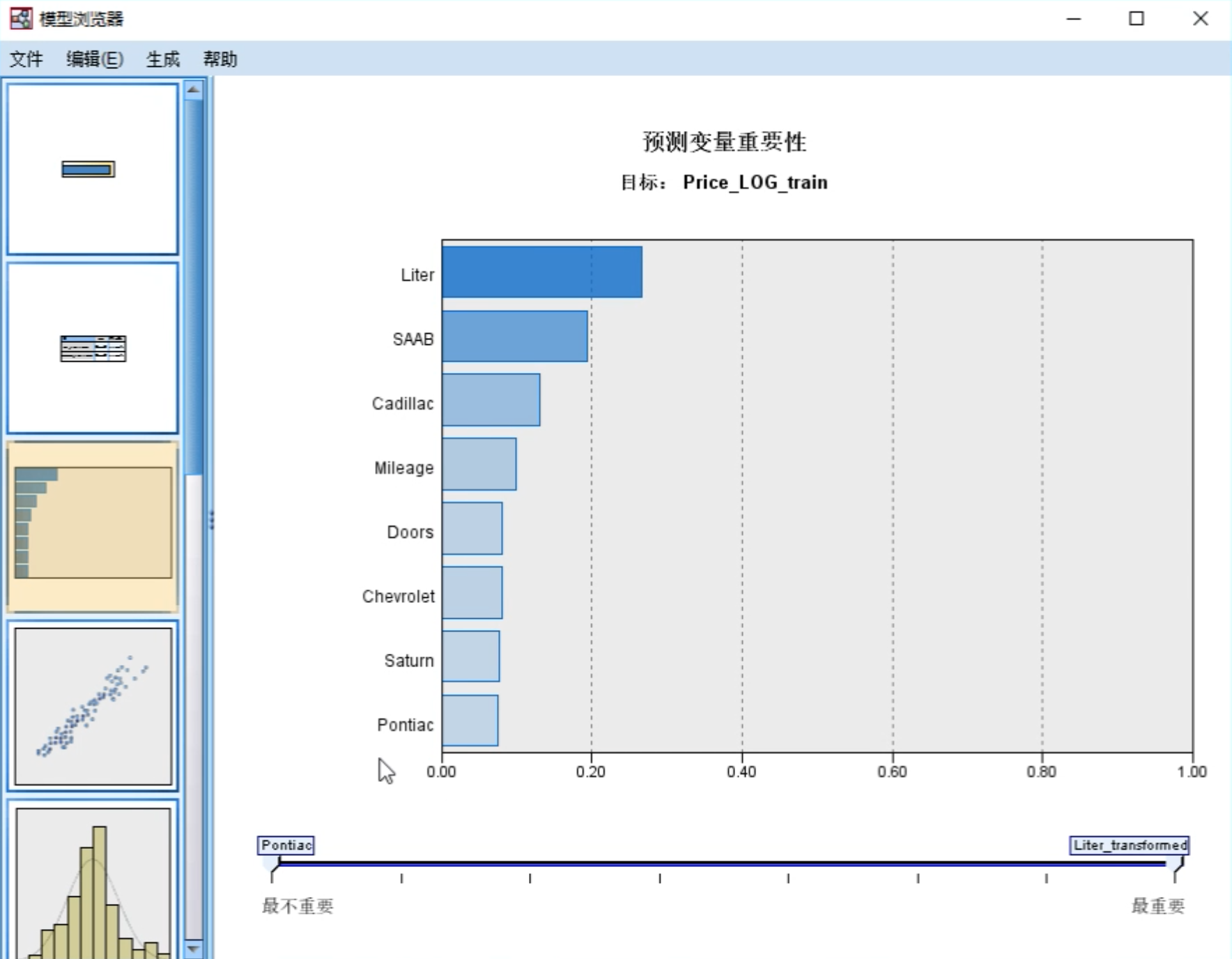
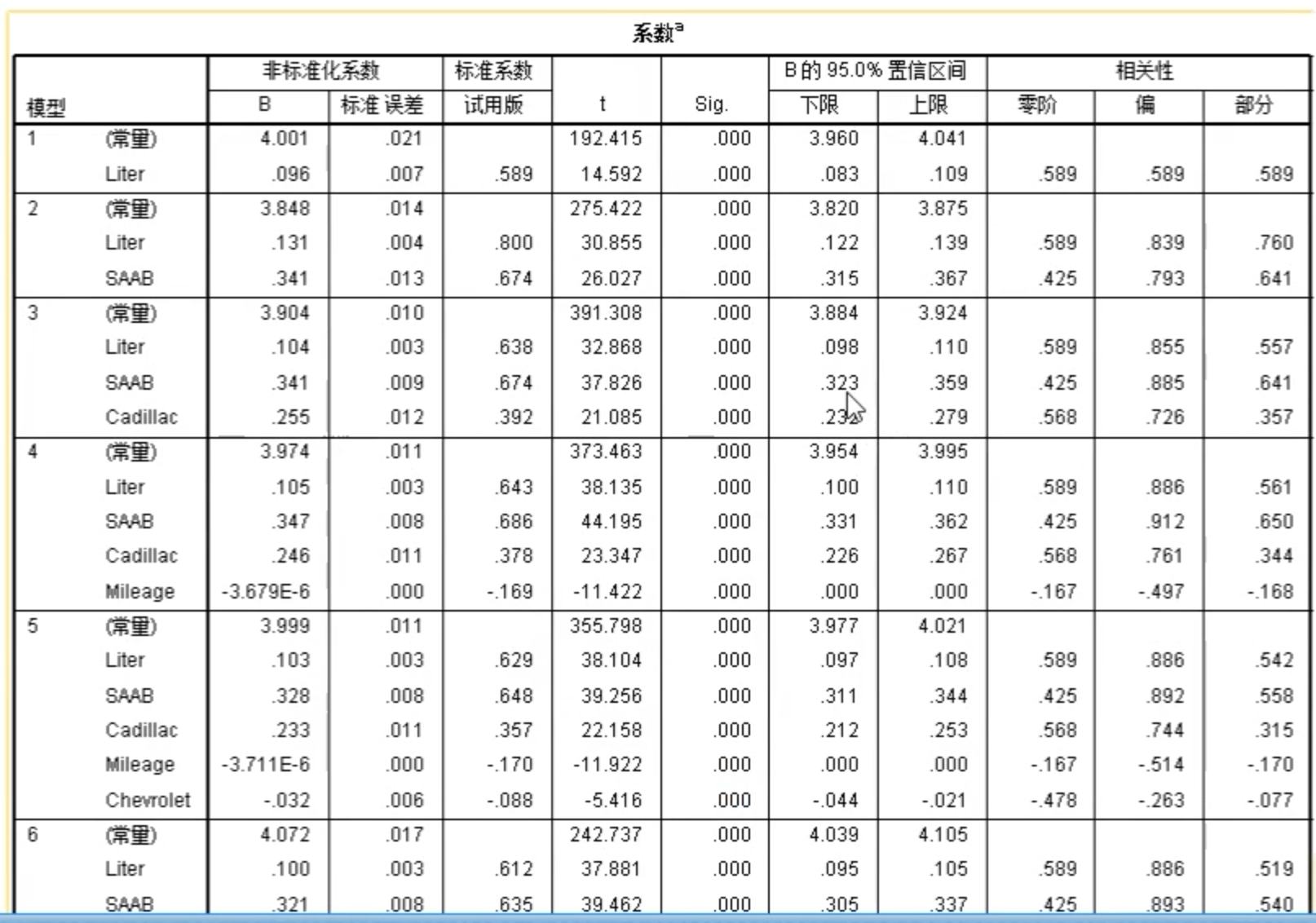
还可以查看各个自变量系数的显著性和重要性。
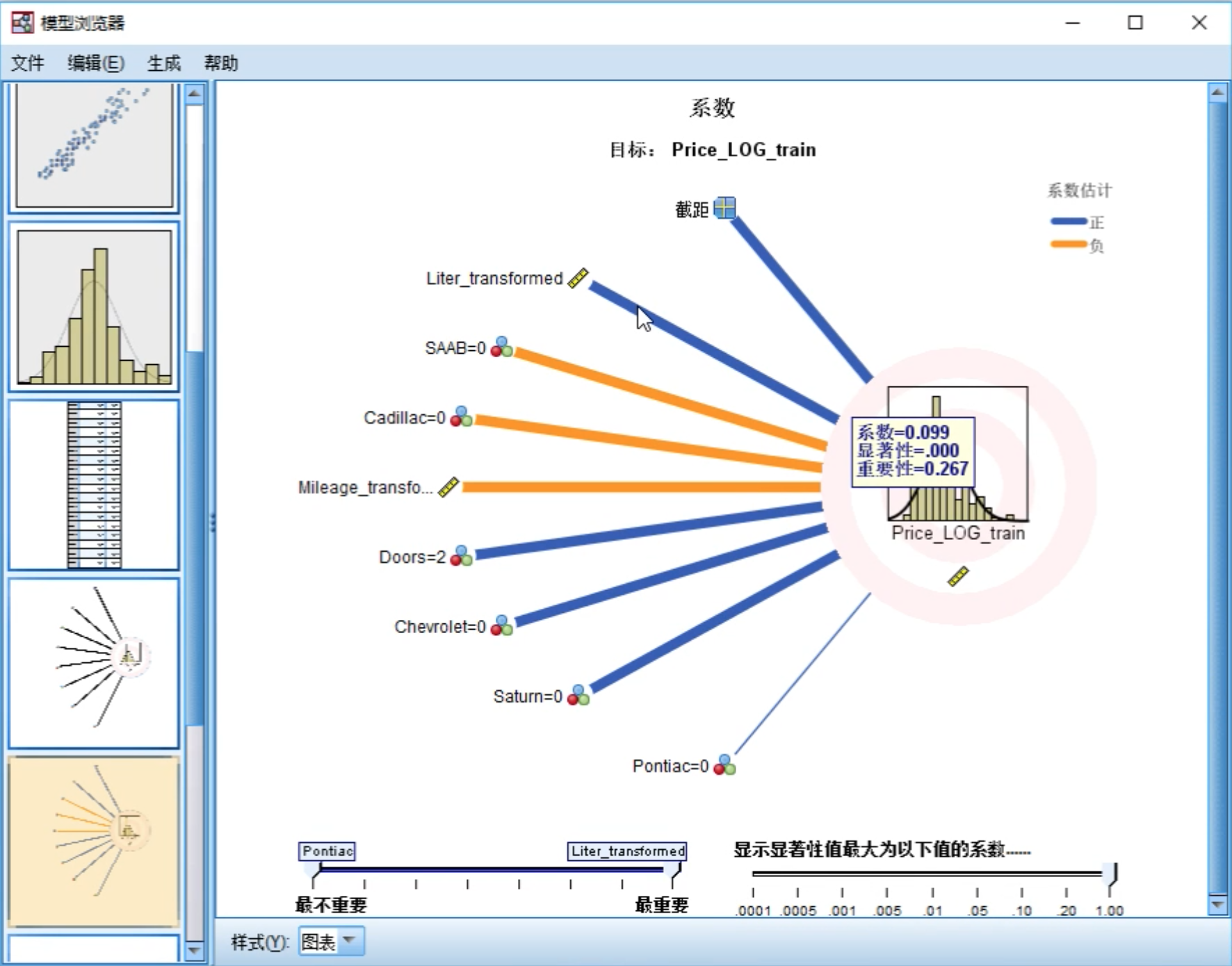
从最终的模型构建结果可以看到,基于当前的准则,哪些自变量属于最优变量(最优子集)。
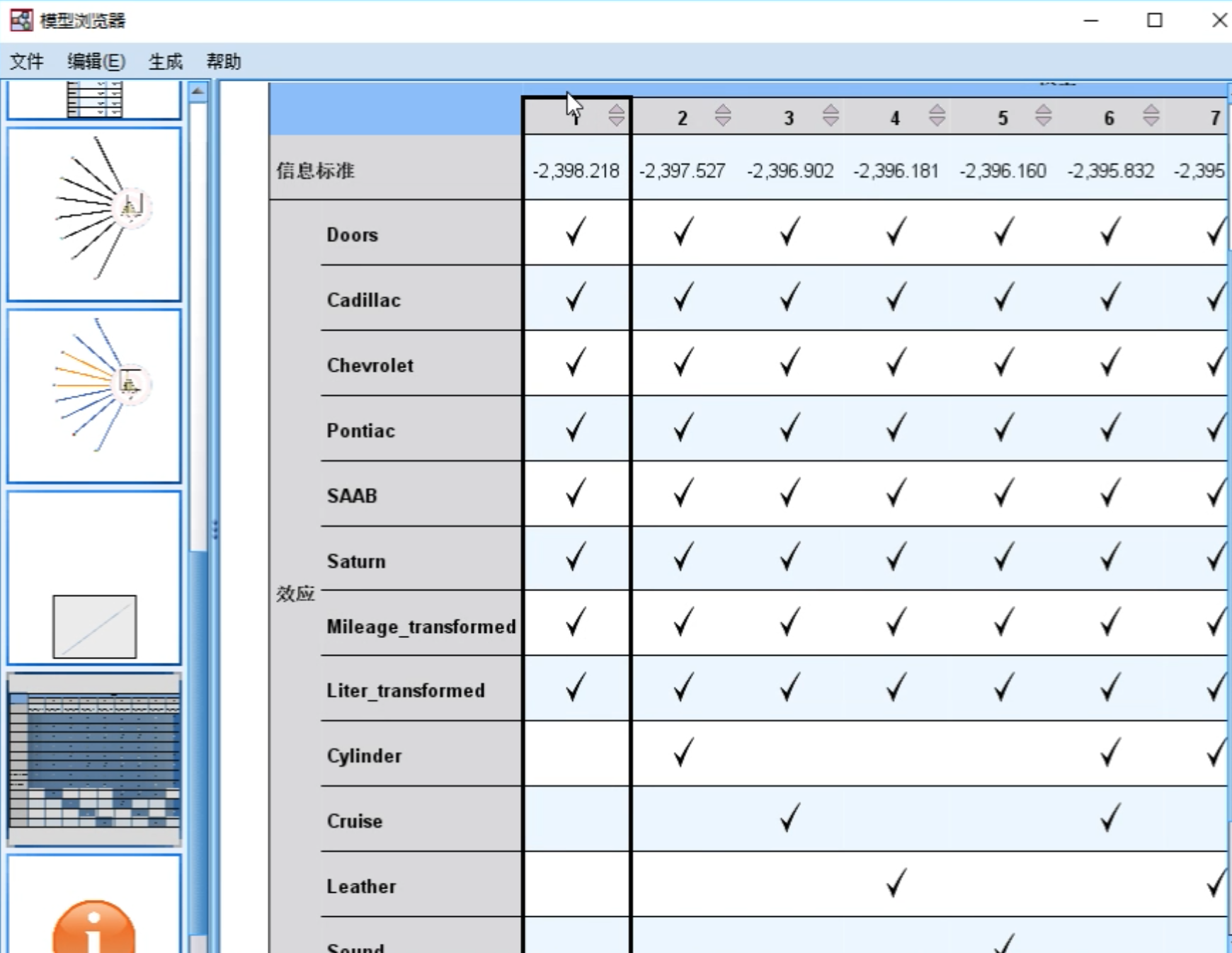
逐步回归
选择工具栏中的分析 -> 线性回归
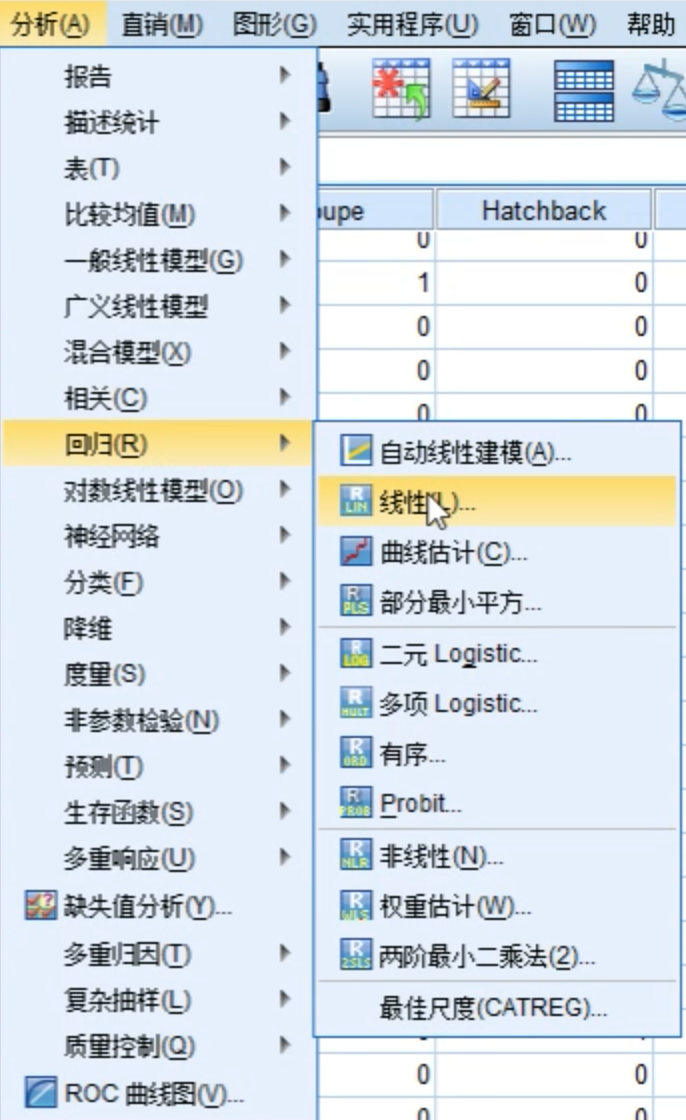
确定因变量和自变量,选择逐步作为回归方法。

设置统计量,可勾选置信区间、D-W、部分相关和偏相关性等选项。

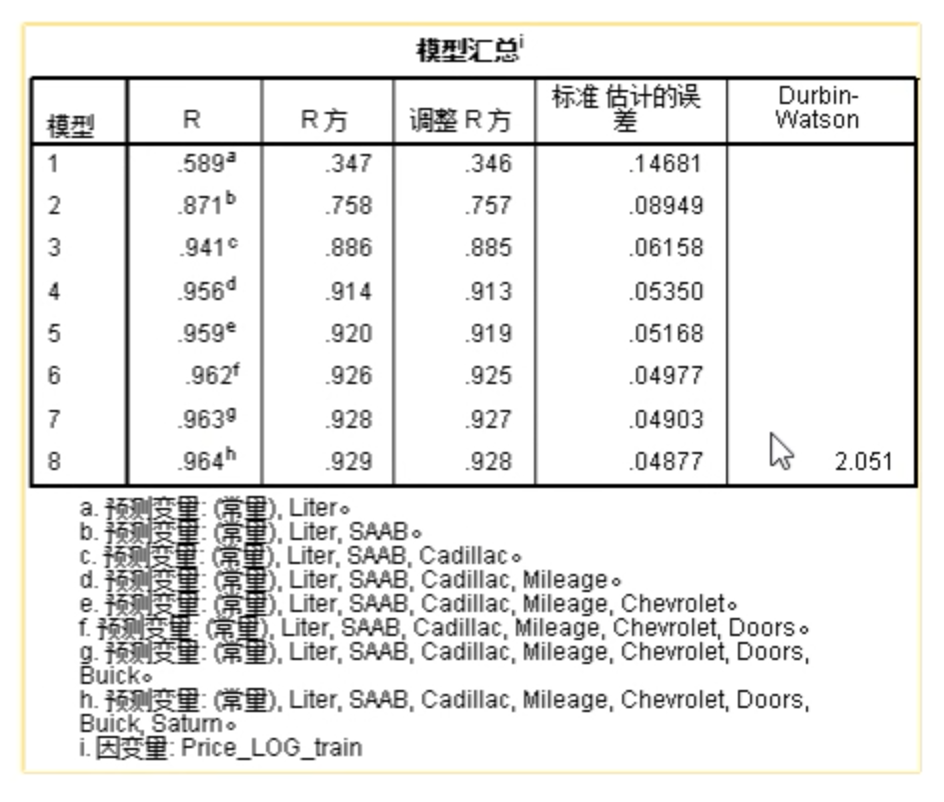
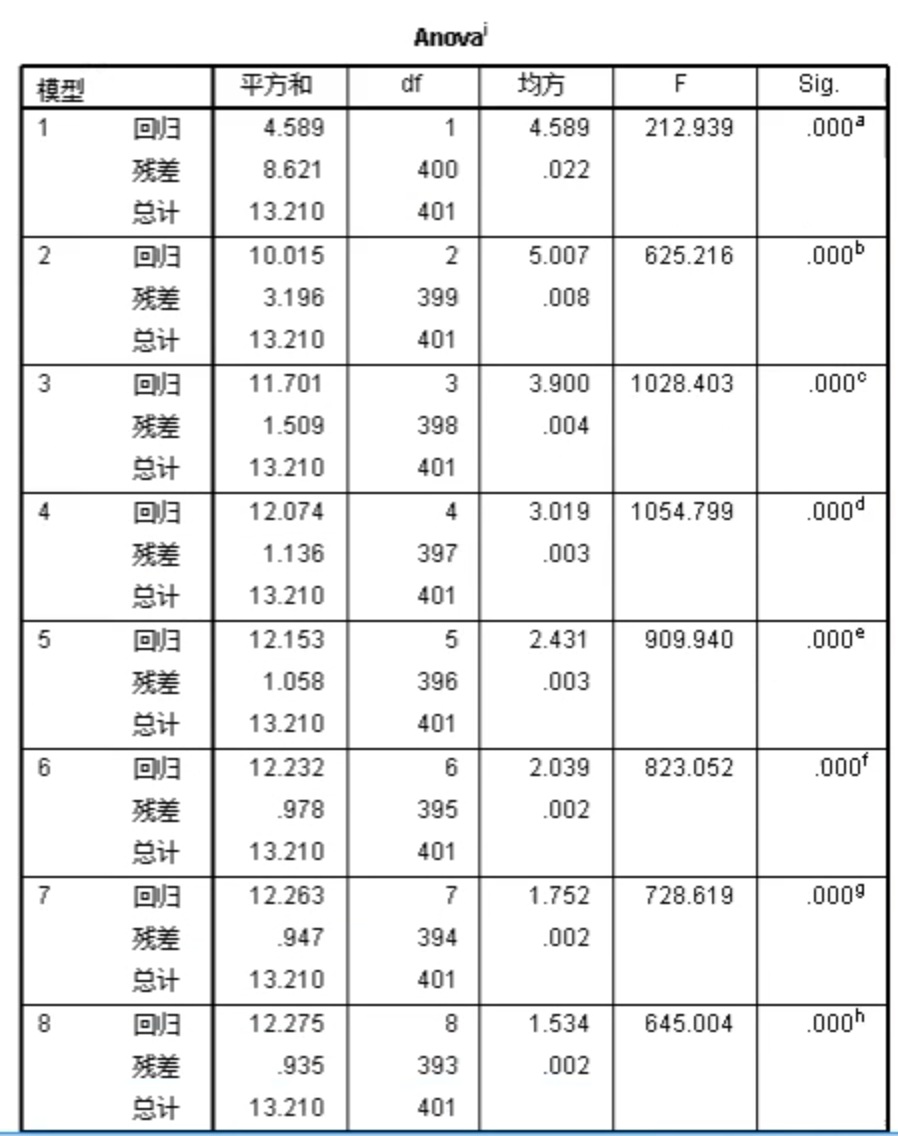
运行模型,从模型汇总结果可以看到每一步的R方(一般看最后一个即可)。
ANOVA表
相关系数表
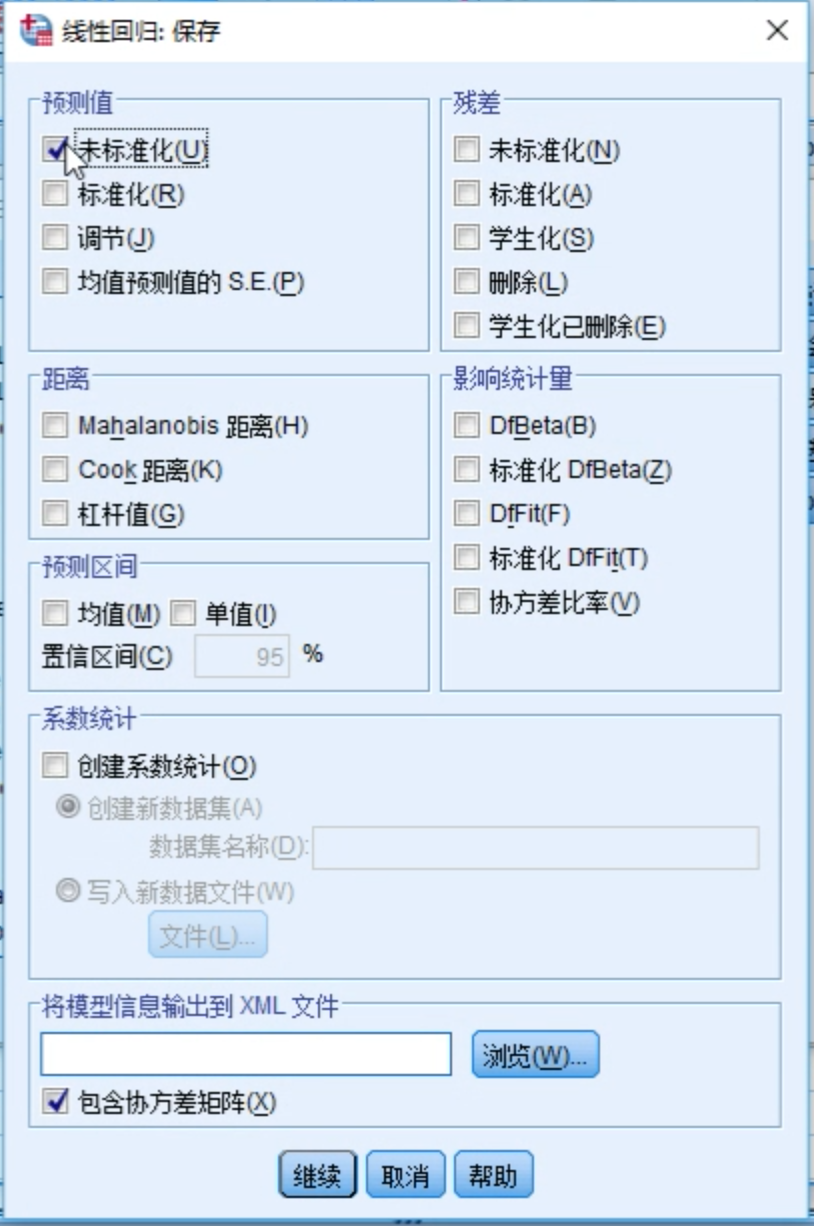
在参数配置时如果勾选了保存 -> 预测值(未标准化)选项,在结果中就会自动生成一列预测值,这样就起到了预测的效果。
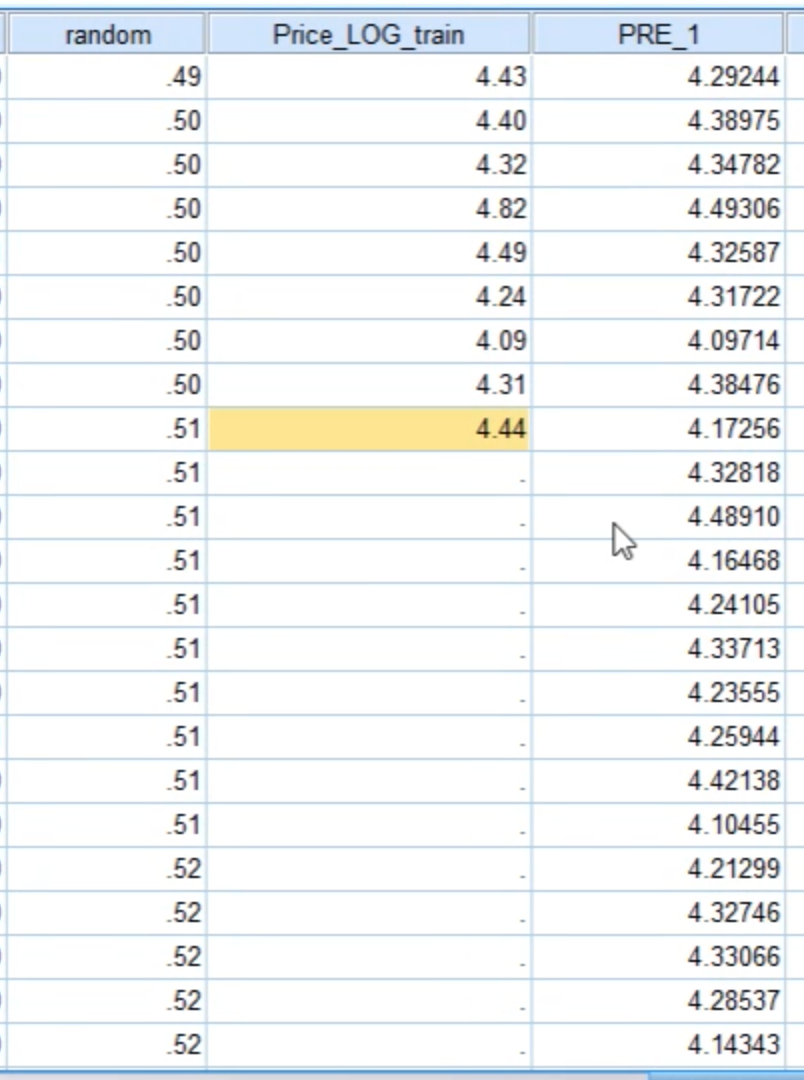
计算误差
将预测结果保存成excel文件,以便在excel中方便地完成误差计算。
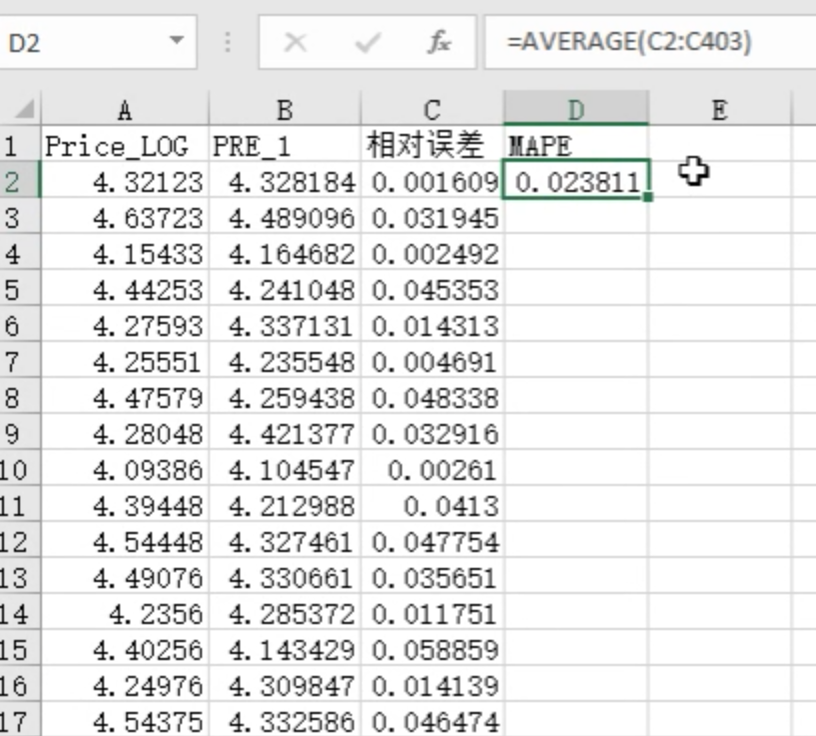
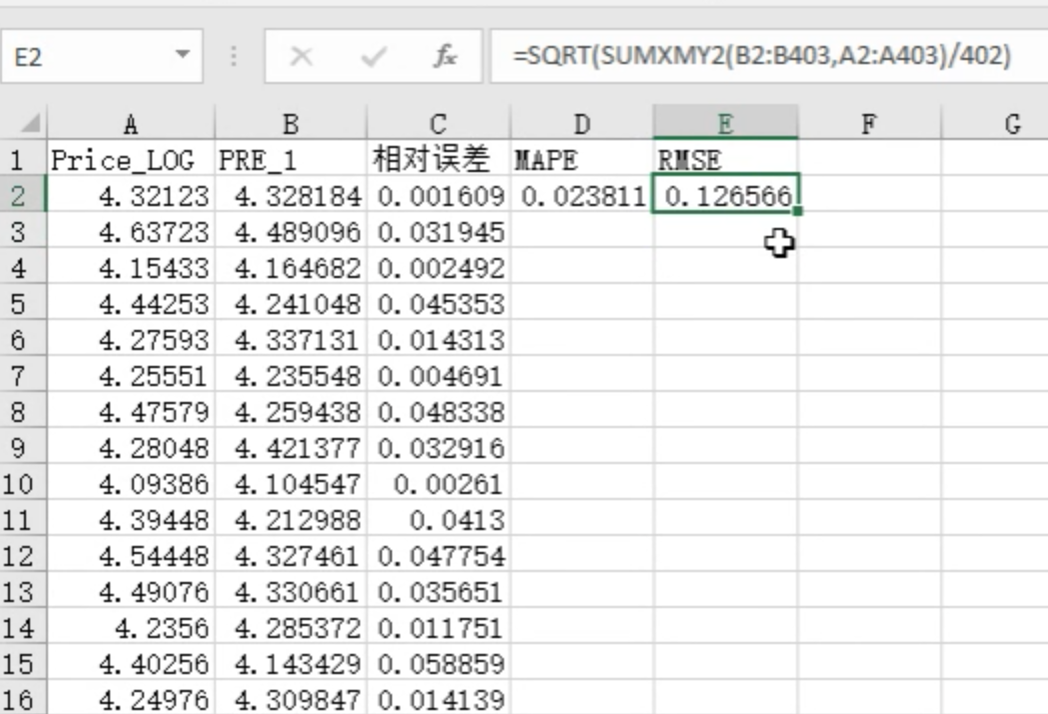
在excel中,我们主要最关心的就是真实值与预测值之间的误差,即Price_LOG与PRE_1
这两列。
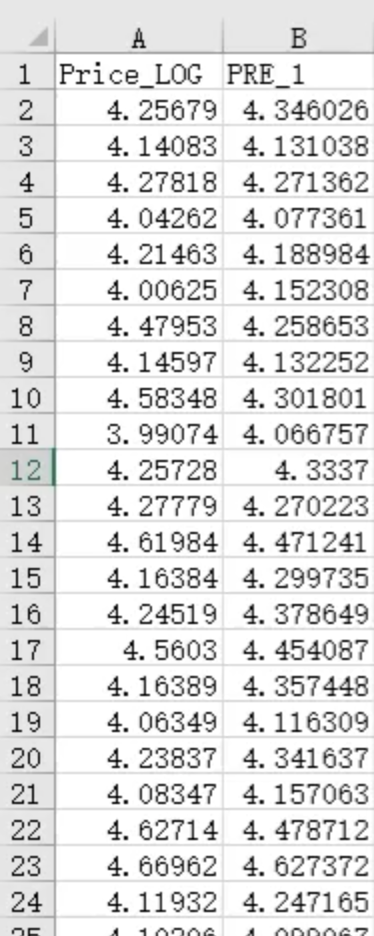
第2-403行数据预测值是我们的模型拟合出来的,删除即可。从第404行开始,是我们真正的预测值。
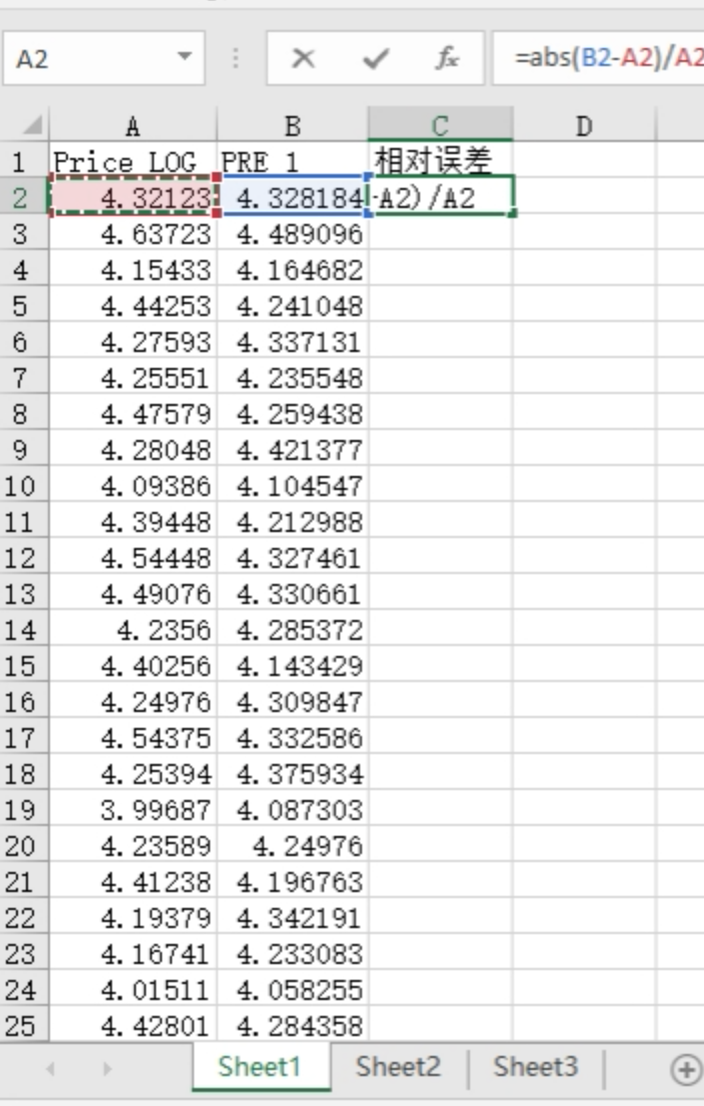
相对误差
相对误差平均值(MAPE)
均方根误差(RMSE)
逻辑回归
训练集和测试集数据分离
总数据700条,将前600条作为训练集,最后100条作为测试集。新建一个计算变量default_model,值从default列中复制。并将最后100条数据删除。
逻辑回归预测
选择分析 -> 回归 -> 二元Logistic进行回归预测
确定因变量和自变量
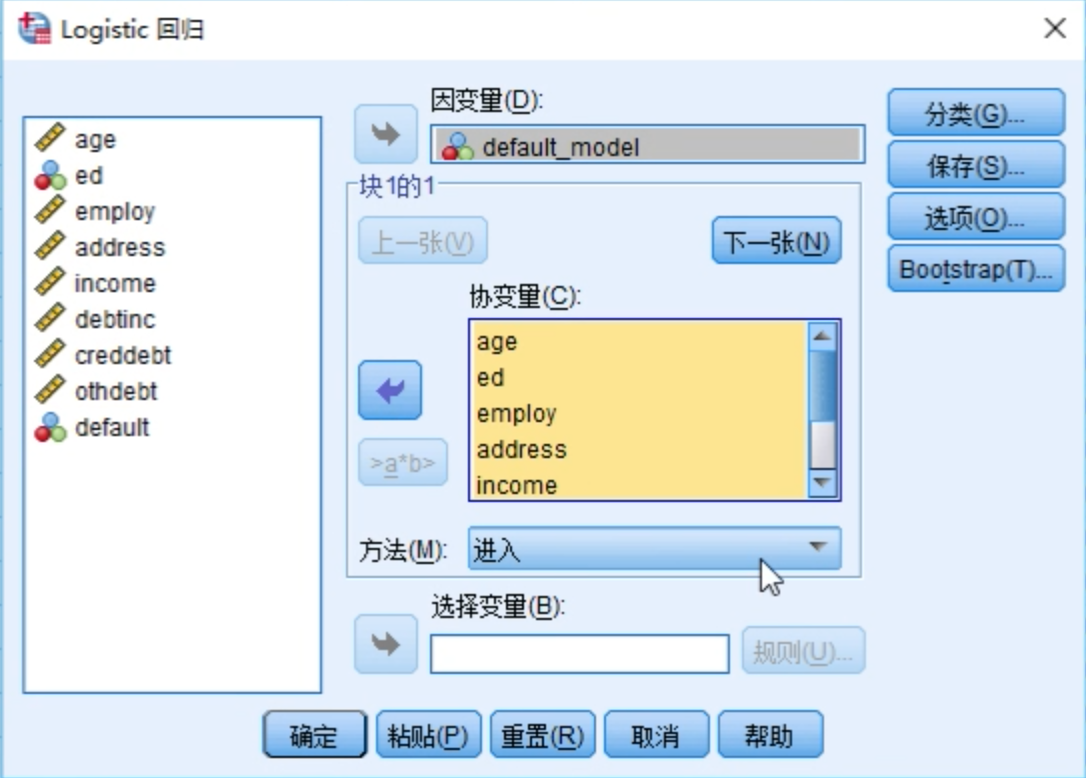
勾选保存选项中的概率和组成员,以便在最终的预测值中体现这两项数值。

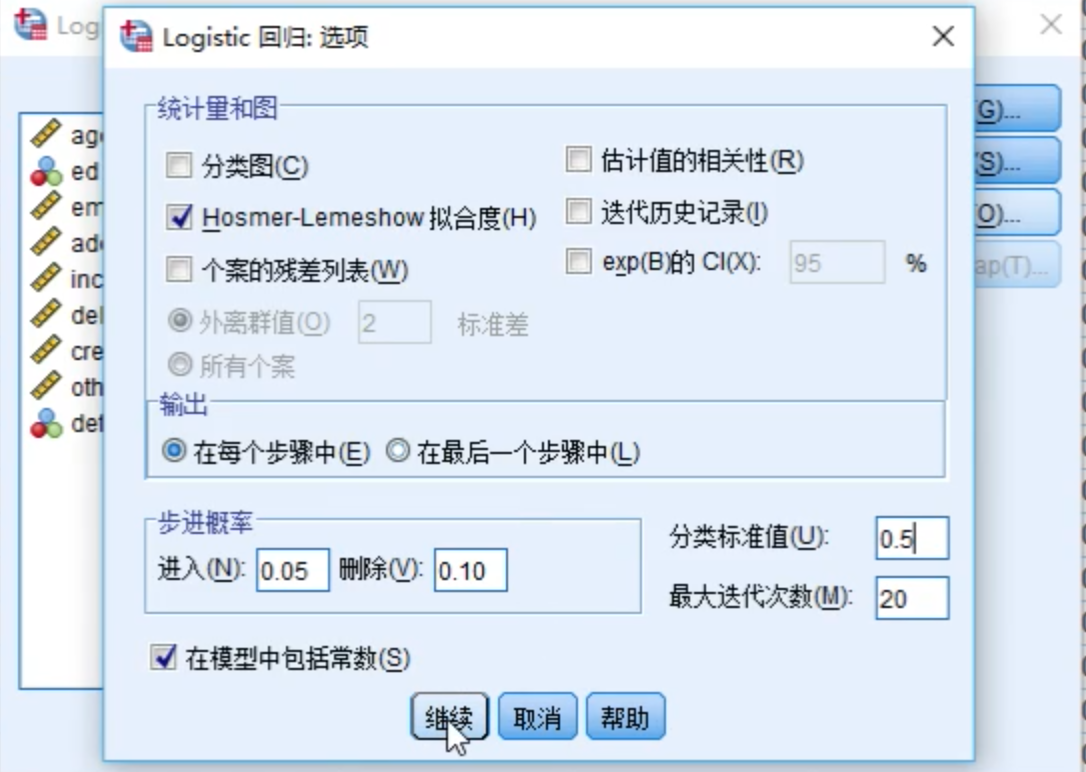
在选项配置中,勾选H-L拟合度,也可以选择只显示最后一步输出,并设置分类标准值(分类依据的阈值,默认0.5)。
结果分析
总共700条数据,其中600条是训练数据,100条预测数据。
模型汇总

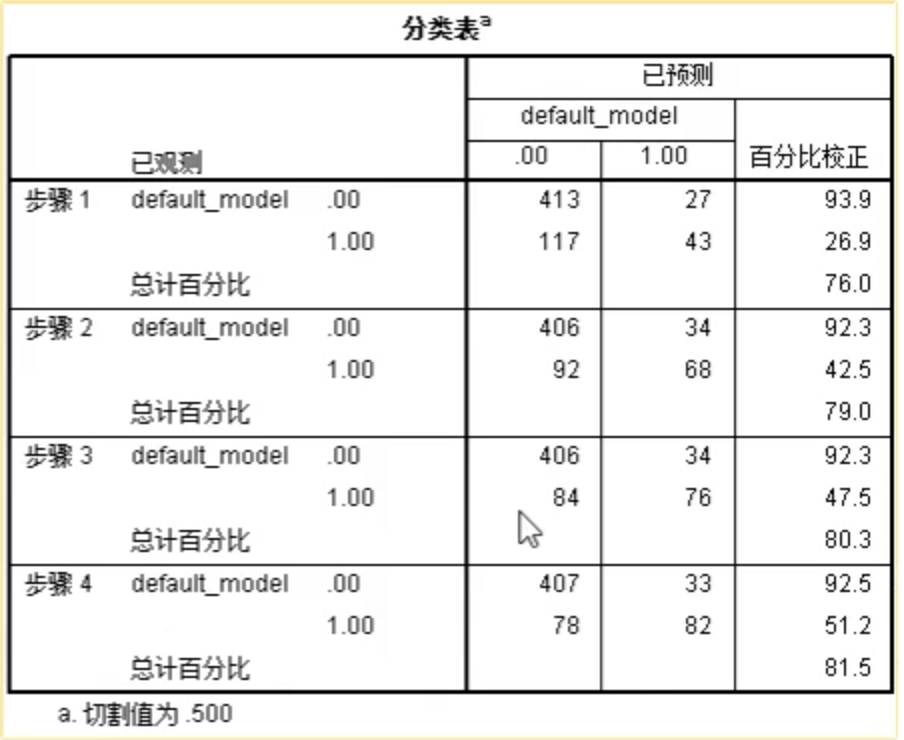
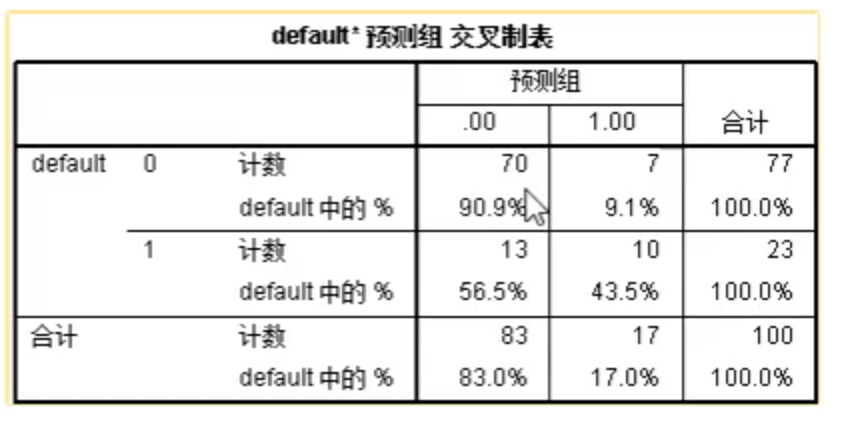
分类表,可重点关注最后一行,可以看到对于600条拟合数据,预测总体的准确率为81.5
从数据结果中可以看到,新生成了两列数据。PRE_1为预测的概率,PGR_1
为预测分组。

可以对100条预测数据的结果进行分析
先将前600条数据排除
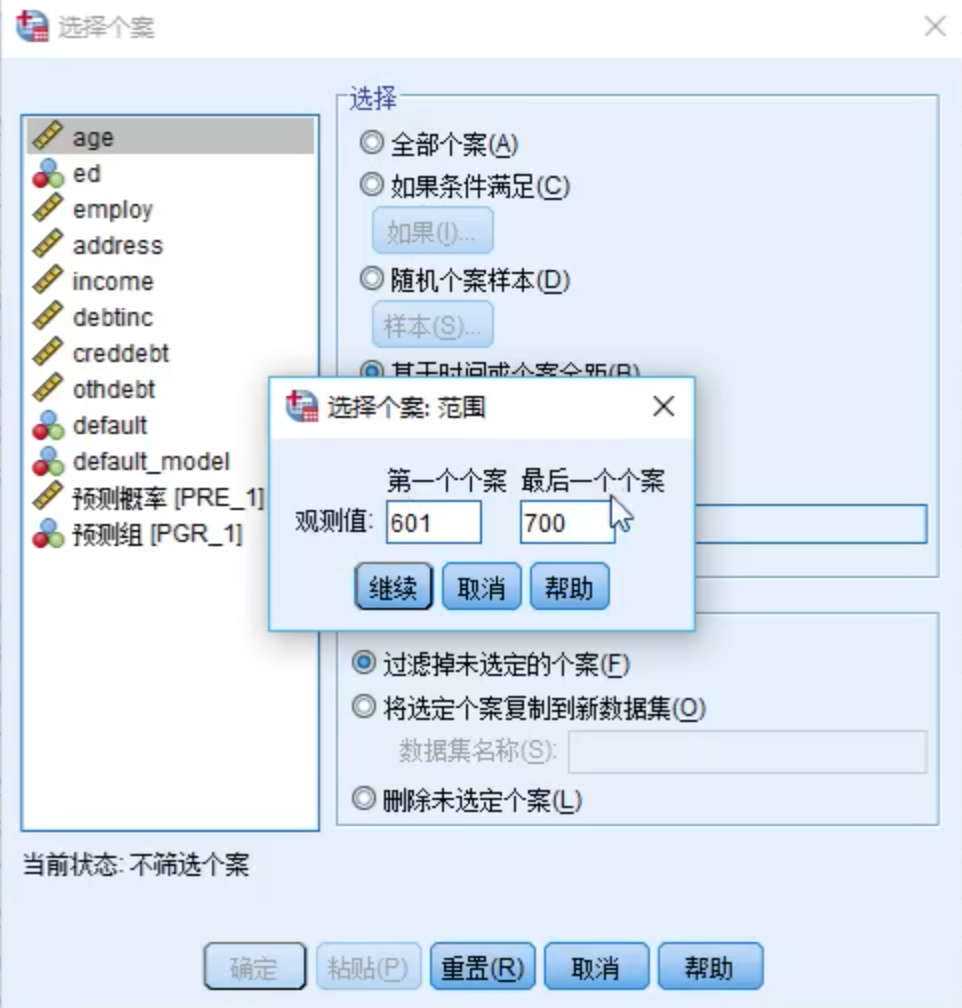
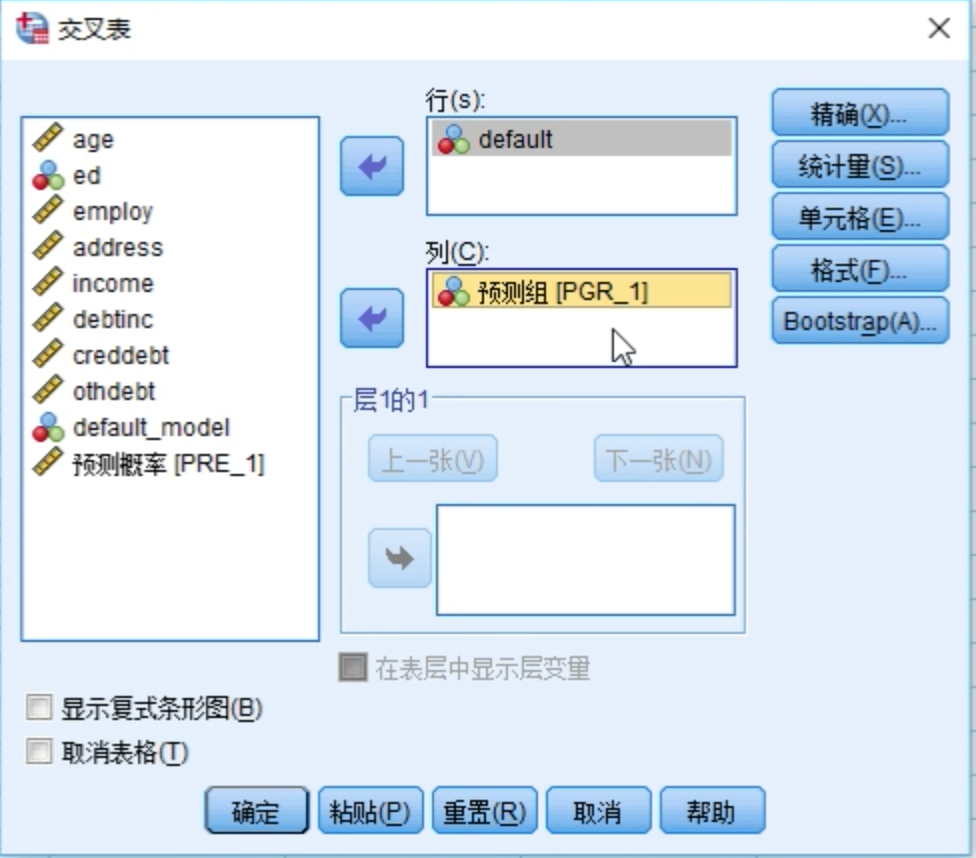
分析 -> 描述统计 -> 交叉表
季节分解和指数平滑法
数据准备
在SPSS中导入社会消费品零售总额数据文件。
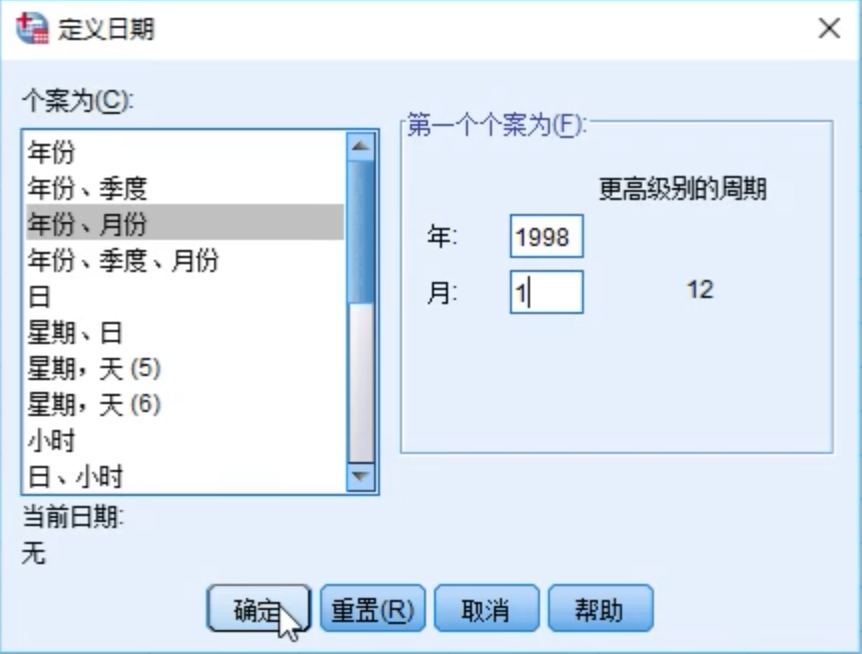
做时间序列第一步,定义日期。
根据数据实际情况设置日期参数
生成的数据结构如下

季节性分解
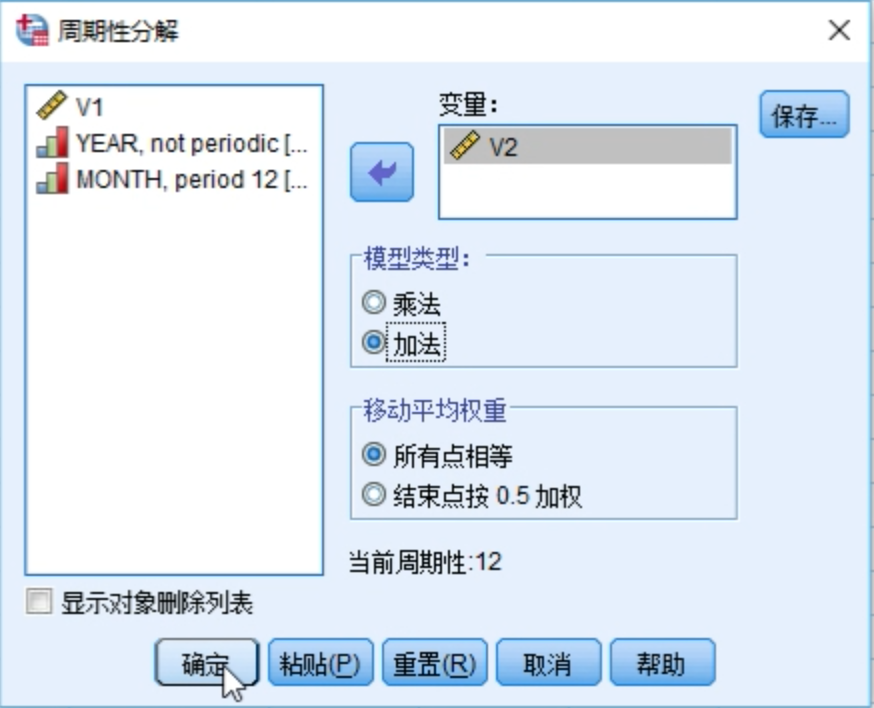
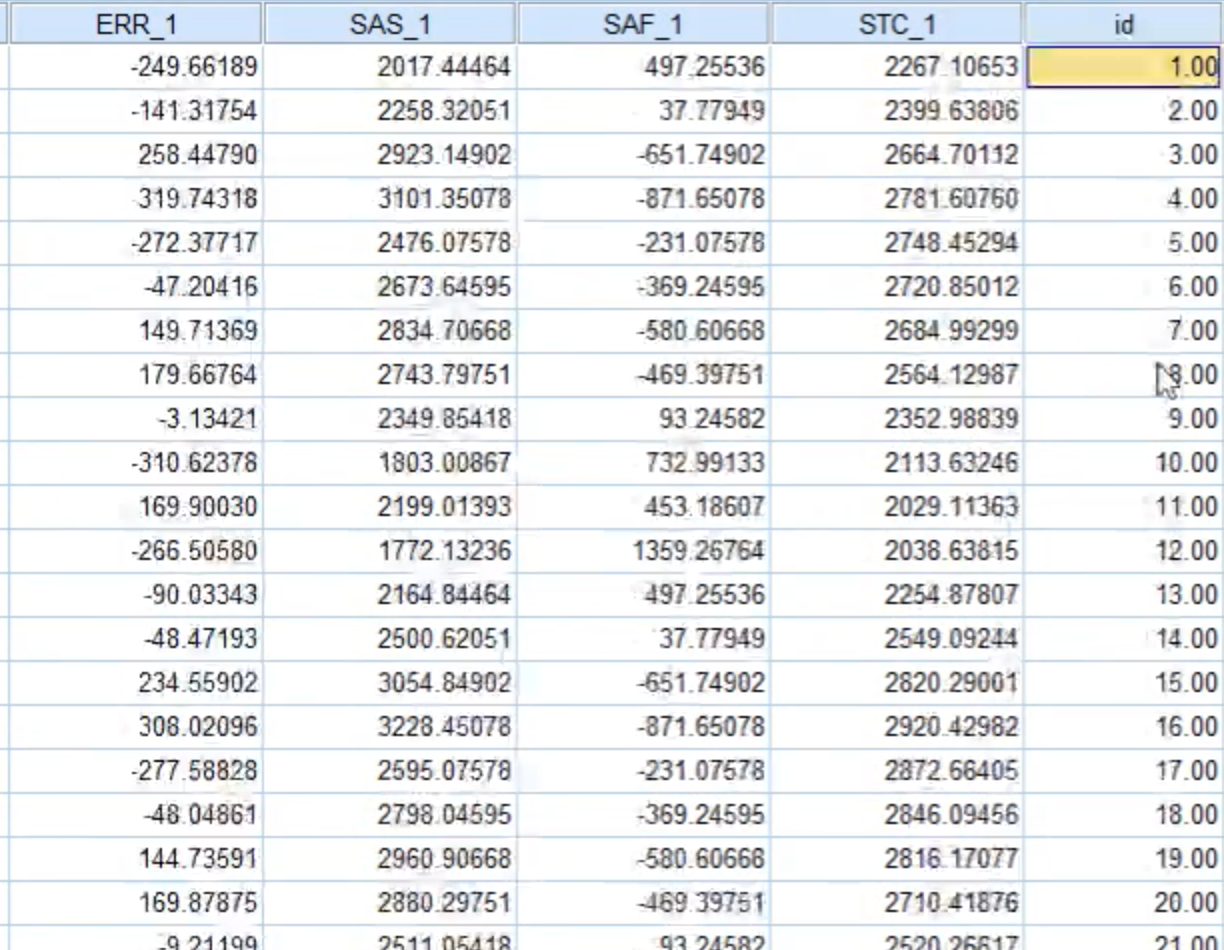
ERR_1: 不规则项SAS_1: 季节性调整项(去掉季节项后的项)SAF_1: 季节项STC_1: 趋势 + 周期
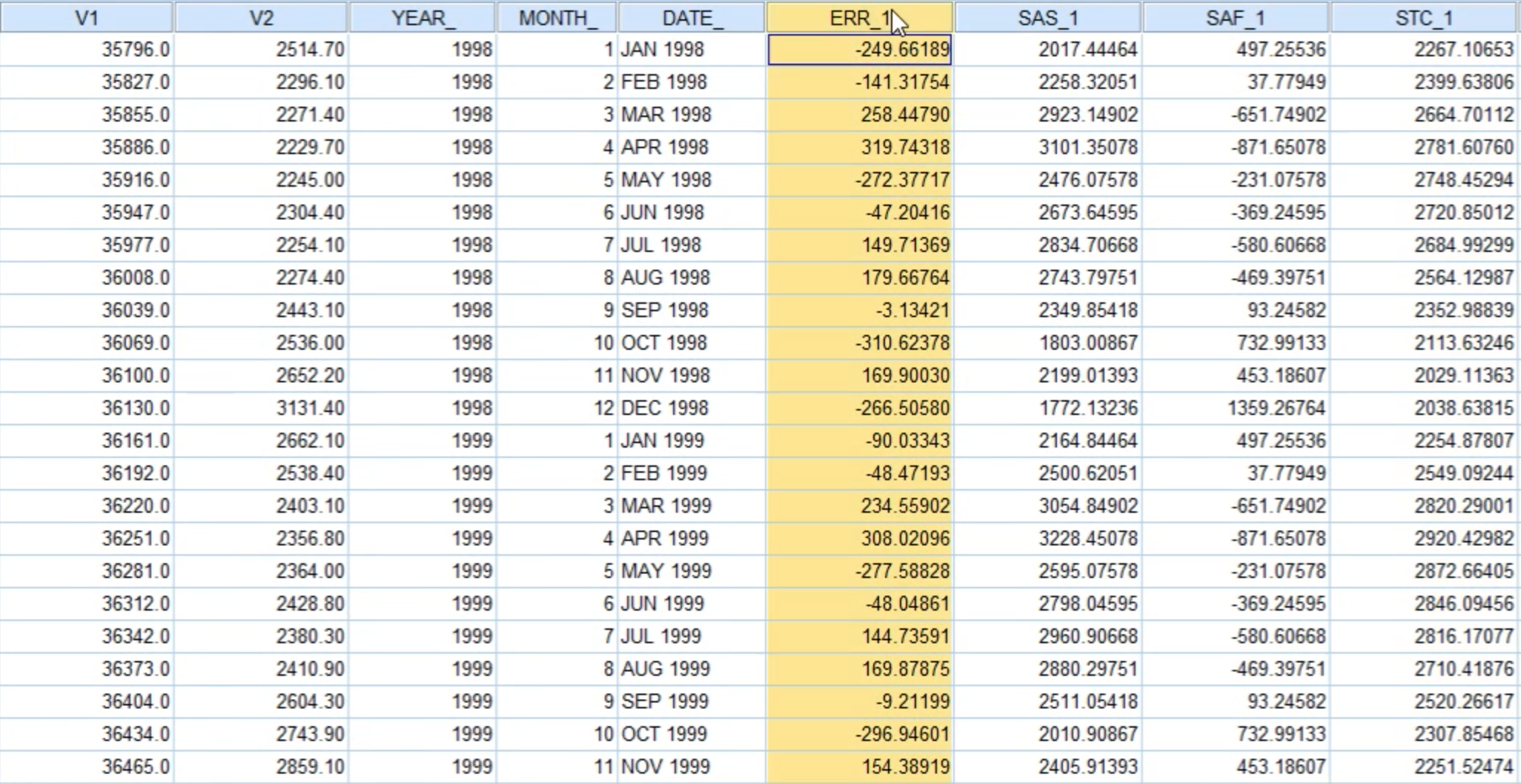
要想画图,还需要增加一个x轴。
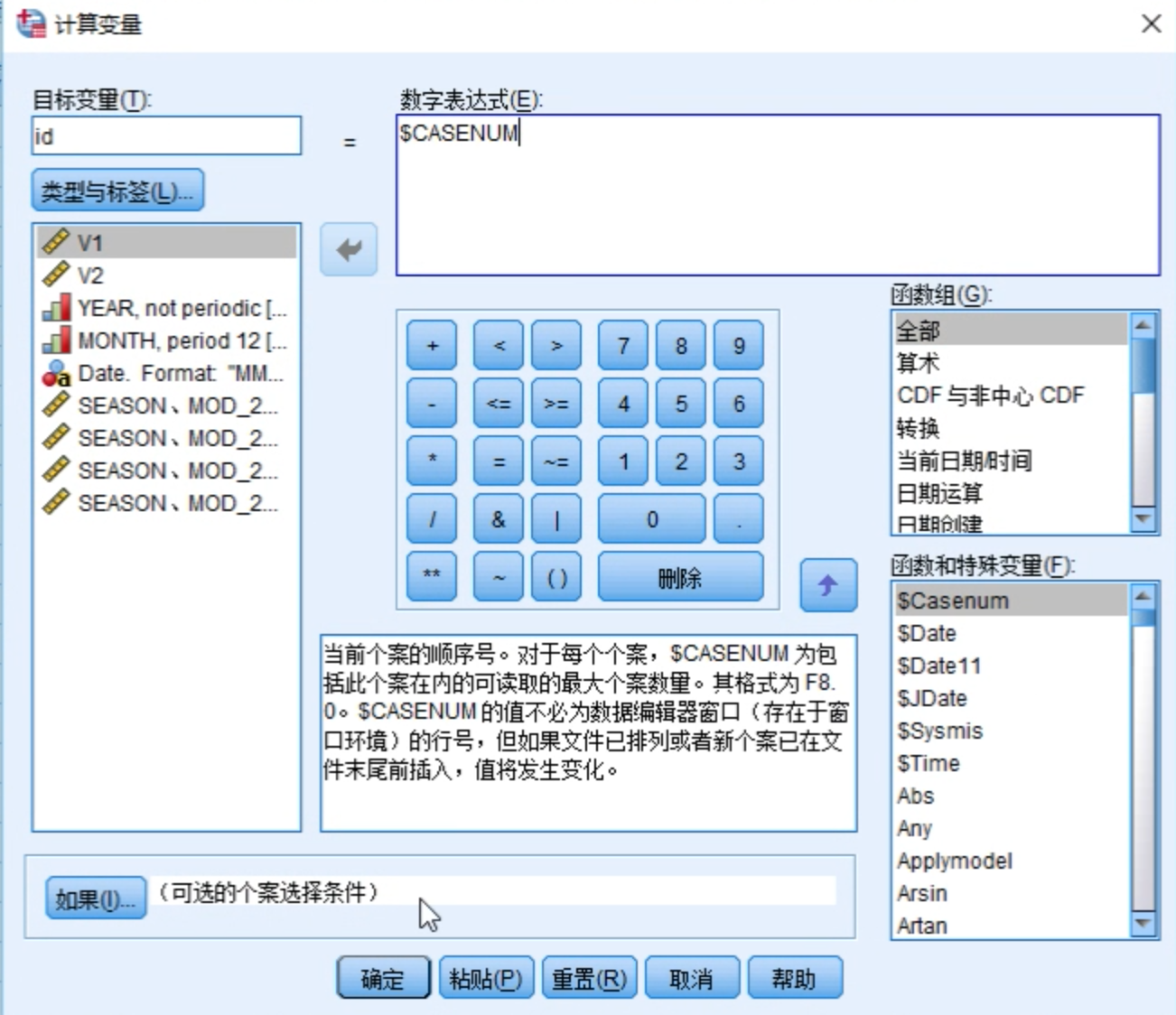

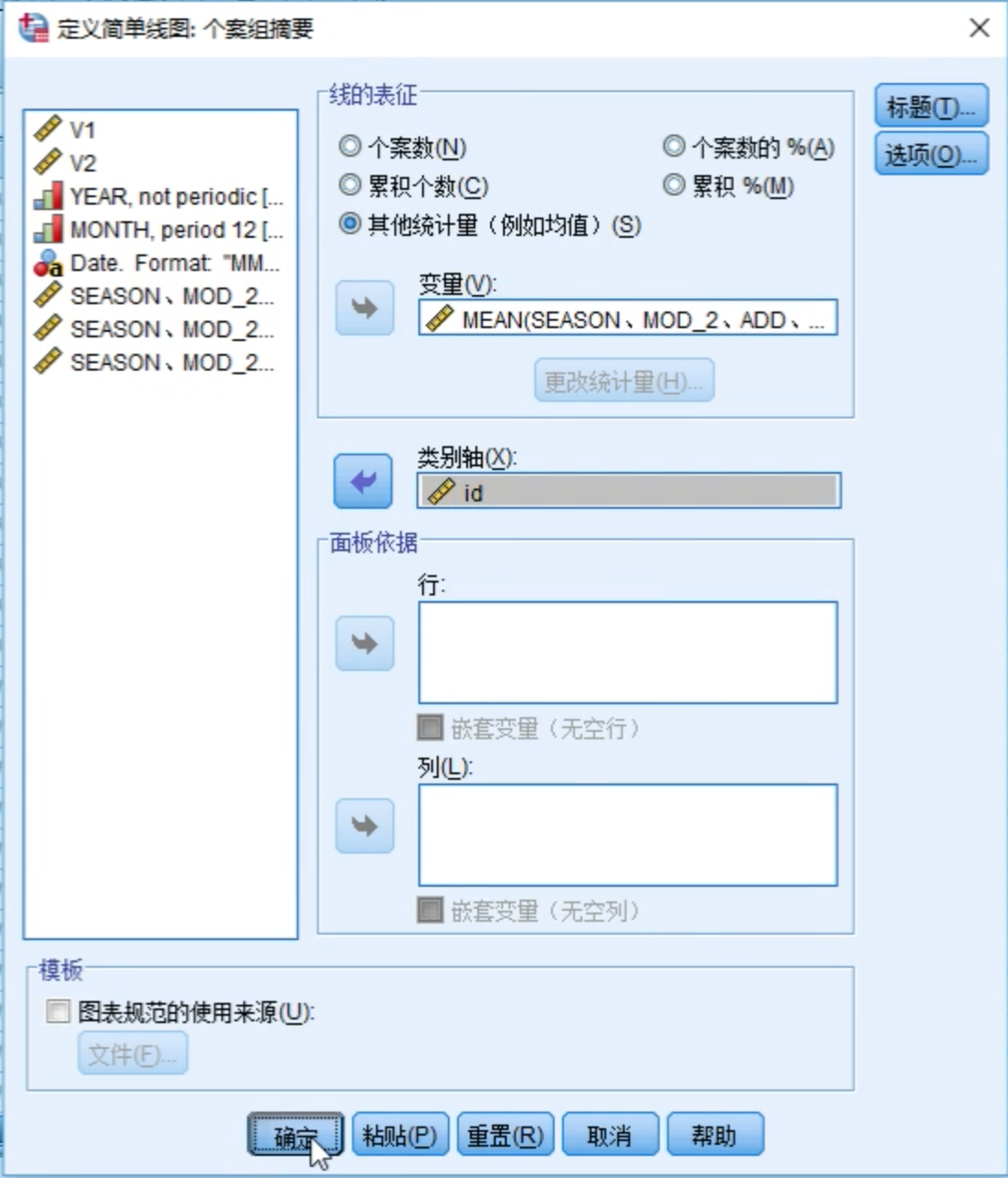
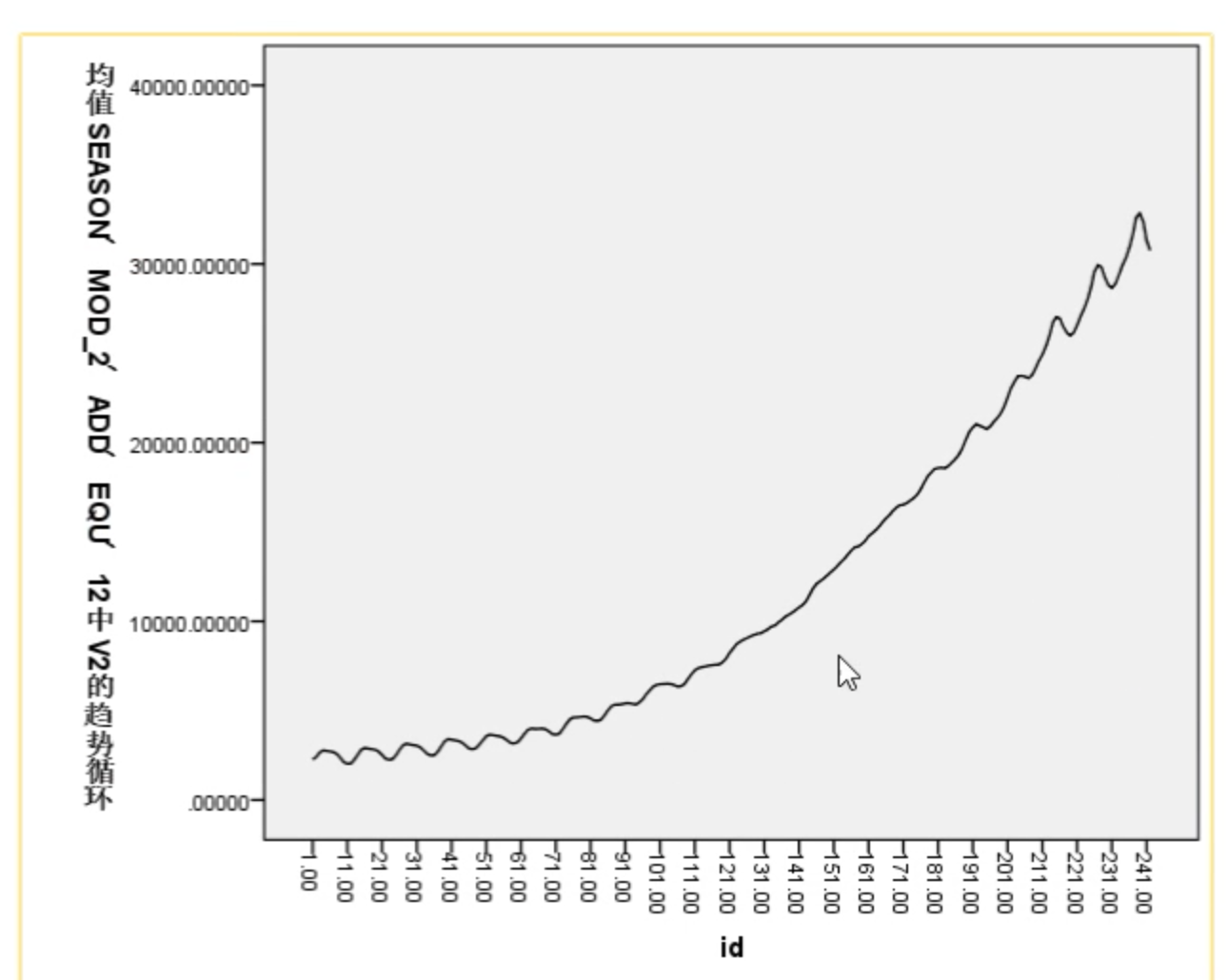
选择趋势 + 周期(第4项)生成图形
选择季节项(第3项)生成图形
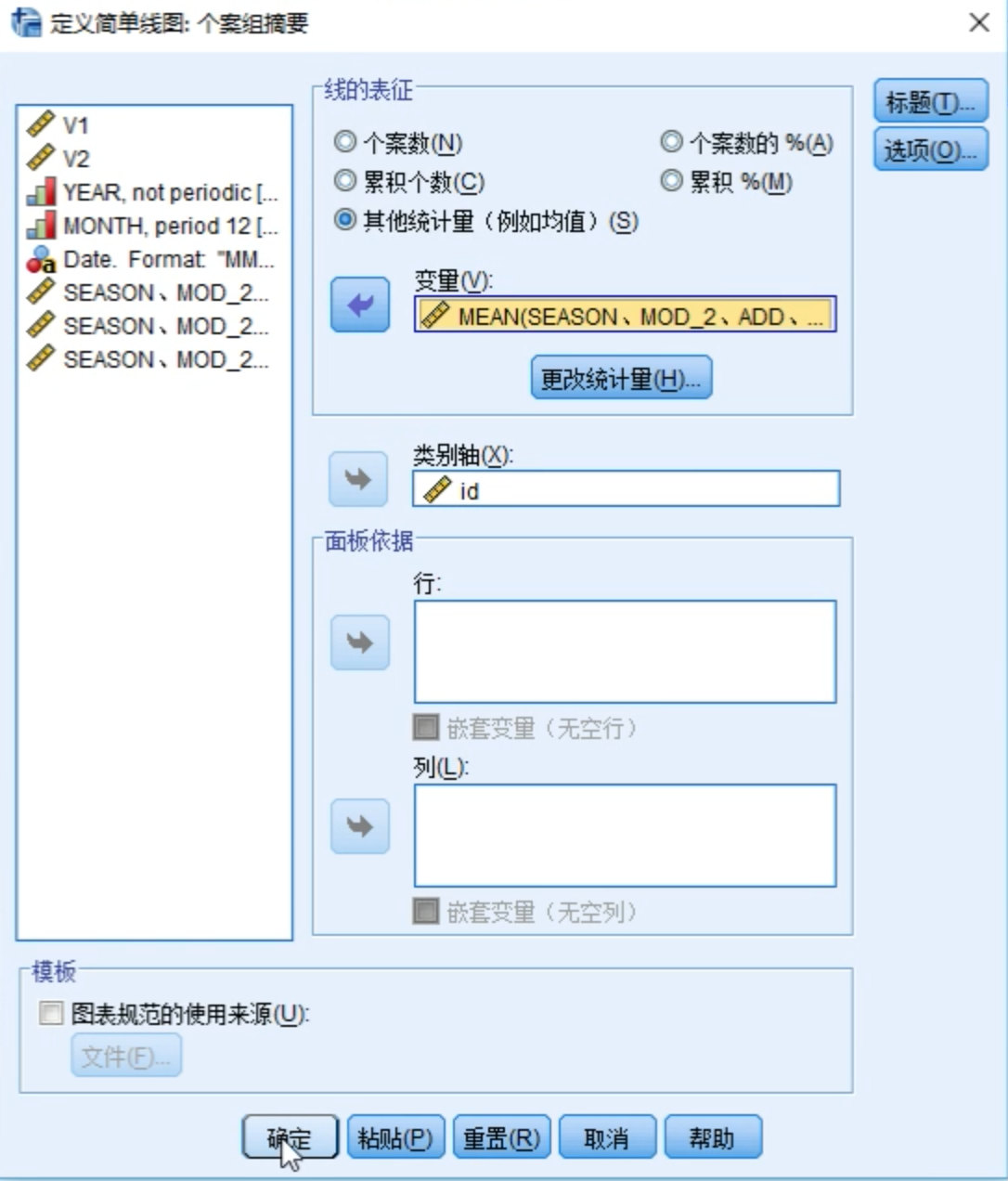

指数平滑法
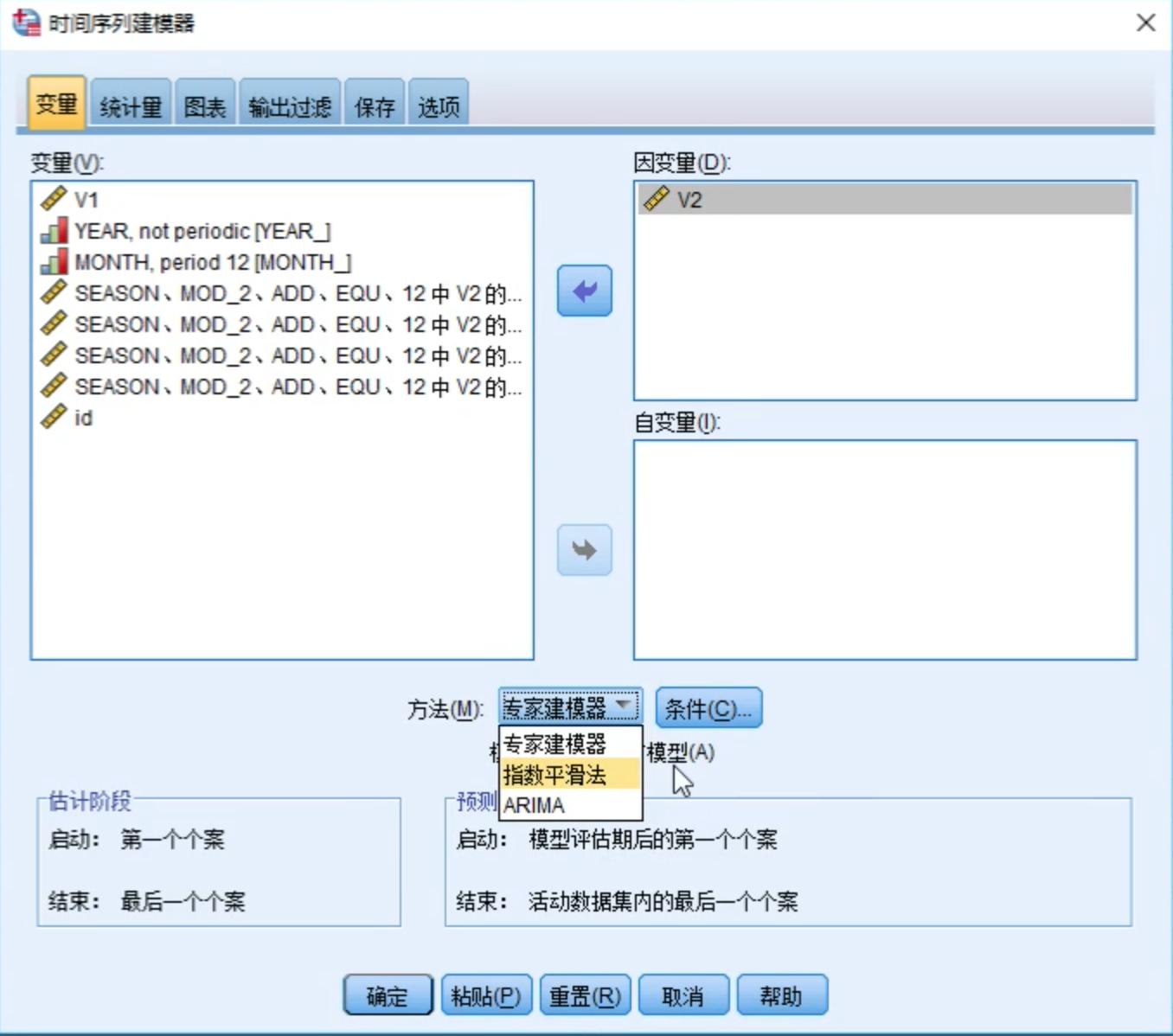
用指数平滑法进行预测

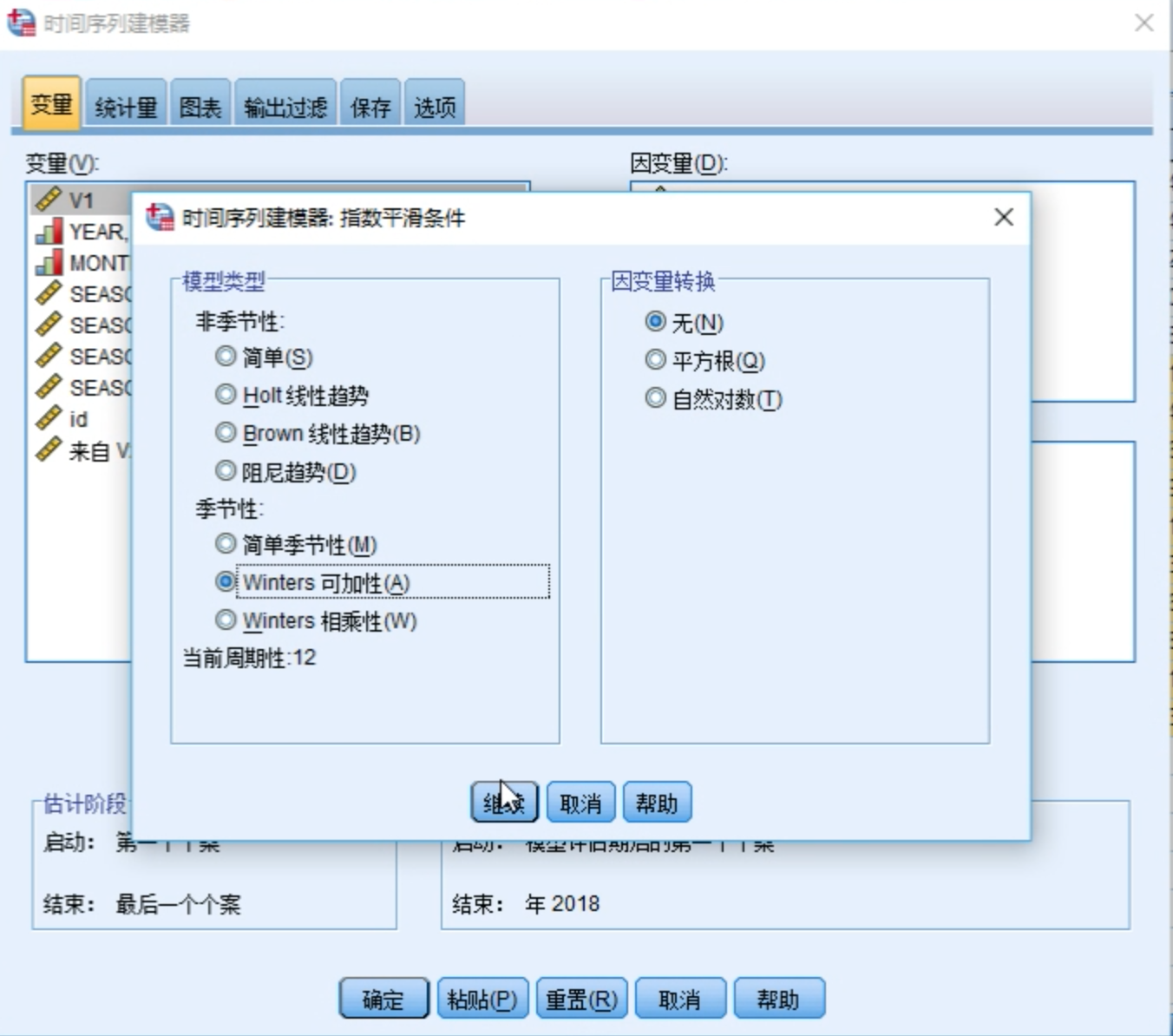
这里选择指数平滑法作为预测方法。如果选择专家建模器,SPSS会自动从指数平滑法和ARIMA里选择最优的。
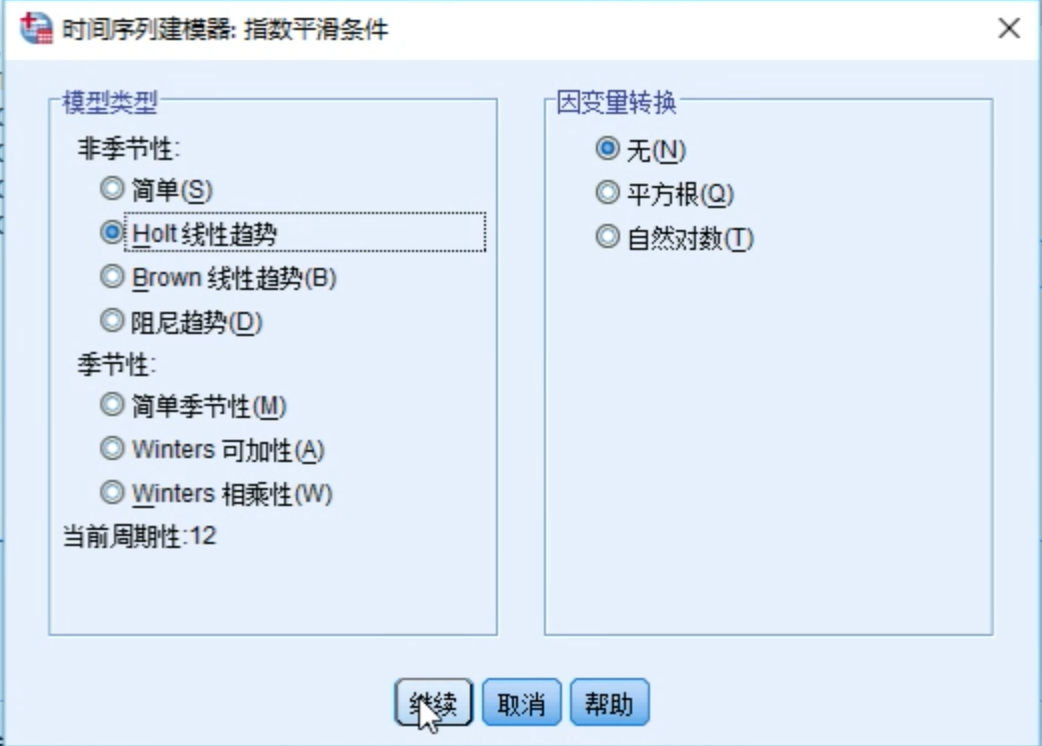
根据需要选择模型类型
勾选拟合值选项

勾选预测值选项
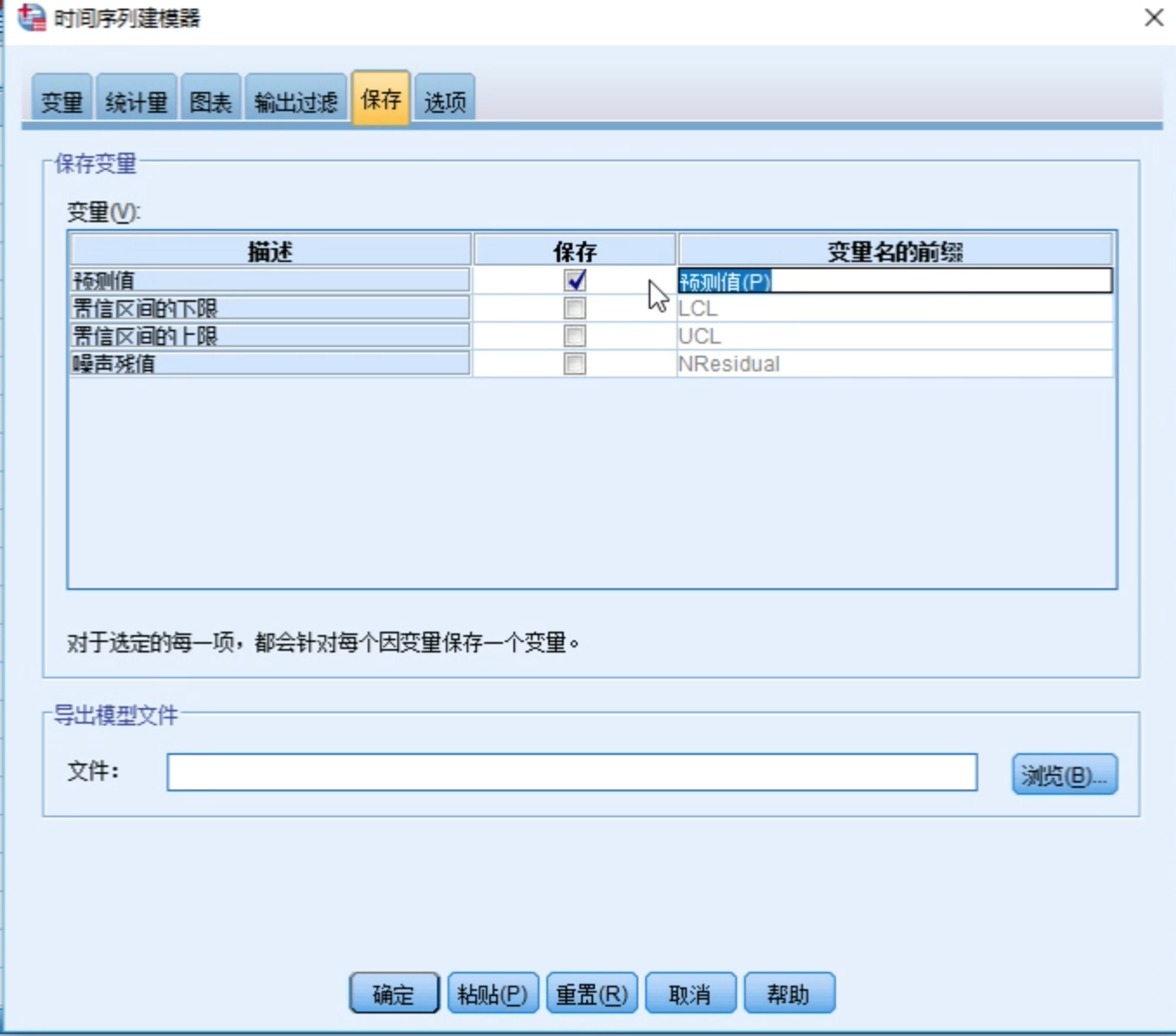
最关键的是选项参数,输入要预测的时间。
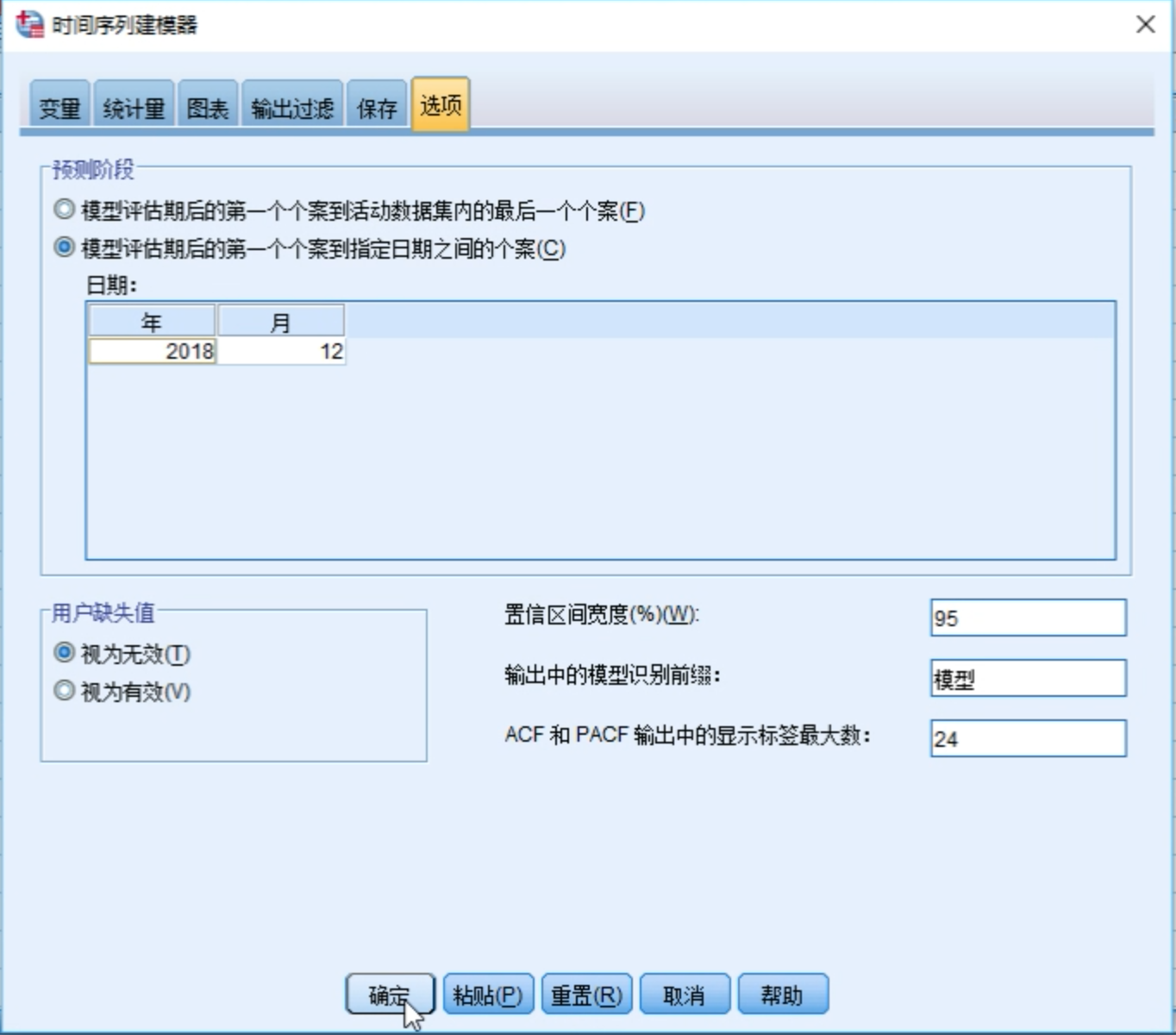
结果如图所示

预测值
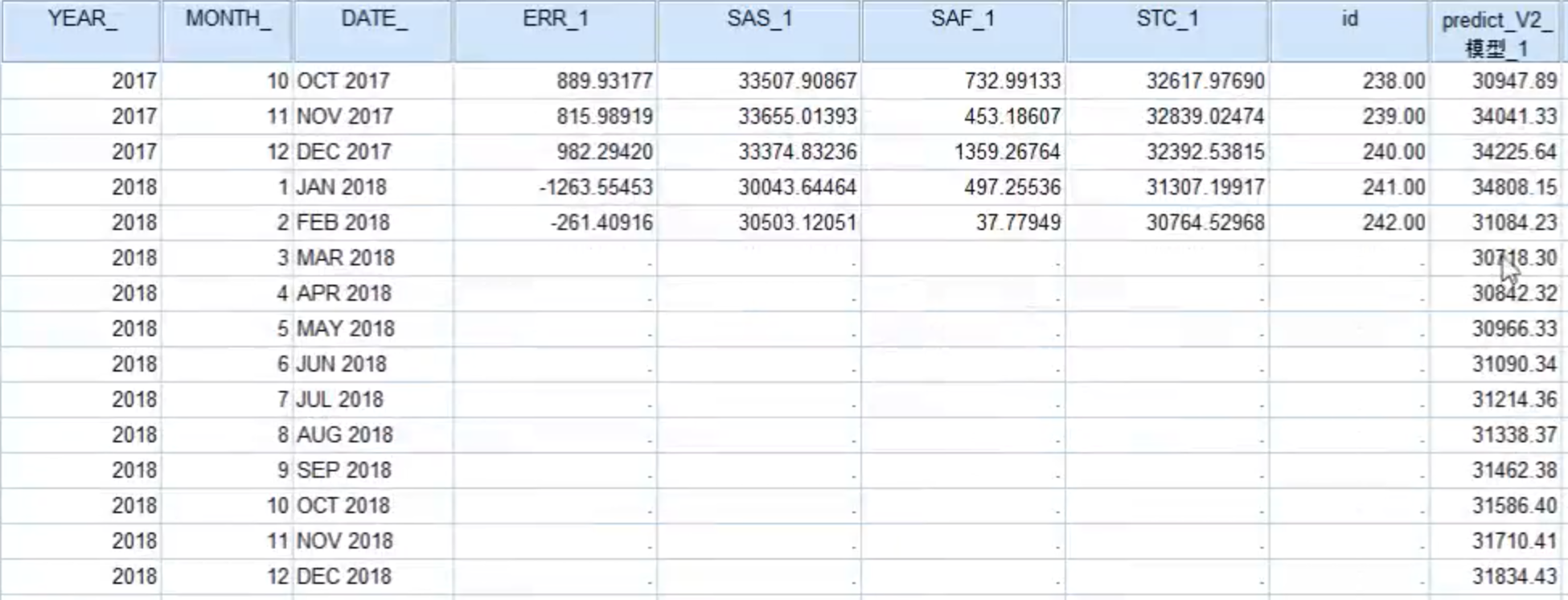
可以调整模型类型,如:选择Winters加法模型